SCI Publications
2023
H. Dai, M. Bauer, P.T. Fletcher, S. Joshi.
“Modeling the Shape of the Brain Connectome via Deep Neural Networks,” In Information Processing in Medical Imaging, Springer Nature Switzerland, pp. 291--302. 2023.
ISBN: 978-3-031-34048-2
The goal of diffusion-weighted magnetic resonance imaging (DWI) is to infer the structural connectivity of an individual subject's brain in vivo. To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. This leads to the challenging problem of estimating a Riemannian metric that is compatible with the DWI data, i.e., a metric such that the geodesic curves represent individual fiber tracts of the connectomics. We reduce this problem to that of solving a highly nonlinear set of partial differential equations (PDEs) and study the applicability of convolutional encoder-decoder neural networks (CEDNNs) for solving this geometrically motivated PDE. Our method achieves excellent performance in the alignment of geodesics with white matter pathways and tackles a long-standing issue in previous geodesic tractography methods: the inability to recover crossing fibers with high fidelity. Code is available at https://github.com/aarentai/Metric-Cnn-3D-IPMI.
2022
H. Dai, M. Bauer, P.T. Fletcher, S.C. Joshi.
“Deep Learning the Shape of the Brain Connectome,” Subtitled “arXiv preprint arXiv:2203.06122, 2022,” 2022.
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.
2021
K. M. Campbell, H. Dai, Z. Su, M. Bauer, P. T. Fletcher, S. C. Joshi.
“Structural Connectome Atlas Construction in the Space of Riemannian Metrics,” Subtitled “arXiv,” 2021.
The structural connectome is often represented by fiber bundles generated from various types of tractography. We propose a method of analyzing connectomes by representing them as a Riemannian metric, thereby viewing them as points in an infinite-dimensional manifold. After equipping this space with a natural metric structure, the Ebin metric, weapply object-oriented statistical analysis to define an atlas as the Fŕechet mean of a population of Riemannian metrics. We demonstrate connectome registration and atlas formation using connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.
K.M. Campbell, H. Dai, Z. Su, M. Bauer, P.T. Fletcher, S.C. Joshi.
“Integrated Construction of Multimodal Atlases with Structural Connectomes in the Space of Riemannian Metrics,” Subtitled “arXiv preprint arXiv:2109.09808,” 2021.
The structural network of the brain, or structural connectome, can be represented by fiber bundles generated by a variety of tractography methods. While such methods give qualitative insights into brain structure, there is controversy over whether they can provide quantitative information, especially at the population level. In order to enable population-level statistical analysis of the structural connectome, we propose representing a connectome as a Riemannian metric, which is a point on an infinite-dimensional manifold. We equip this manifold with the Ebin metric, a natural metric structure for this space, to get a Riemannian manifold along with its associated geometric properties. We then use this Riemannian framework to apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. This formulation ties into the existing framework for diffeomorphic construction of image atlases, allowing us to construct a multimodal atlas by simultaneously integrating complementary white matter structure details from DWMRI and cortical details from T1-weighted MRI. We illustrate our framework with 2D data examples of connectome registration and atlas formation. Finally, we build an example 3D multimodal atlas using T1 images and connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.
2019
K. A. Johnson, P. T. Fletcher, D. Servello, A. Bona, M. Porta, J. L. Ostrem, E. Bardinet, M. Welter, A. M. Lozano, J. C. Baldermann, J. Kuhn, D. Huys, T. Foltynie, M. Hariz, E. M. Joyce, L. Zrinzo, Z. Kefalopoulou, J. Zhang, F. Meng, C. Zhang, Z. Ling, X. Xu, X. Yu, A. YJM Smeets, L. Ackermans, V. Visser-Vandewalle, A. Y. Mogilner, M. H. Pourfar, L. Almeida, A. Gunduz, W. Hu, K. D. Foote, M. S. Okun, C. R. Butson.
“Image-based analysis and long-term clinical outcomes of deep brain stimulation for Tourette syndrome: a multisite study,” In Journal of Neurology, Neurosurgery & Psychiatry, BMJ Publishing Group, 2019.
DOI: 10.1136/jnnp-2019-320379
BACKGROUND:
Deep brain stimulation (DBS) can be an effective therapy for tics and comorbidities in select cases of severe, treatment-refractory Tourette syndrome (TS). Clinical responses remain variable across patients, which may be attributed to differences in the location of the neuroanatomical regions being stimulated. We evaluated active contact locations and regions of stimulation across a large cohort of patients with TS in an effort to guide future targeting.
2017
S. Palande, V. Jose, B. Zielinski, J. Anderson, P.T. Fletcher, B. Wang.
“Revisiting Abnormalities in Brain Network Architecture Underlying Autism Using Topology-Inspired Statistical Inference,” In Connectomics in NeuroImaging, Springer International Publishing, pp. 98--107. 2017.
DOI: 10.1007/978-3-319-67159-8_12
A large body of evidence relates autism with abnormal structural and functional brain connectivity. Structural covariance MRI (scMRI) is a technique that maps brain regions with covarying gray matter density across subjects. It provides a way to probe the anatomical structures underlying intrinsic connectivity networks (ICNs) through the analysis of the gray matter signal covariance. In this paper, we apply topological data analysis in conjunction with scMRI to explore network-specific differences in the gray matter structure in subjects with autism versus age-, gender- and IQ-matched controls. Specifically, we investigate topological differences in gray matter structures captured by structural covariance networks (SCNs) derived from three ICNs strongly implicated in autism, namely, the salience network (SN), the default mode network (DMN) and the executive control network (ECN). By combining topological data analysis with statistical inference, our results provide evidence of statistically significant network-specific structural abnormalities in autism, from SCNs derived from SN and ECN. These differences in brain architecture are consistent with direct structural analysis using scMRI (Zielinski et al. 2012).
2016
Y. Gao, M. Zhang, K. Grewen, P. T. Fletcher, G. Gerig.
“Image registration and segmentation in longitudinal MRI using temporal appearance modeling,” In 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), IEEE, pp. 629--632. April, 2016.
DOI: 10.1109/isbi.2016.7493346
P. Muralidharan, J. Fishbaugh, E. Y. Kim, H. J. Johnson, J. S. Paulsen, G. Gerig, P. T. Fletcher.
“Bayesian Covariate Selection in Mixed Effects Models for Longitudinal Shape Analysis,” In International Symposium on Biomedical Imaging (ISBI), IEEE, April, 2016.
DOI: 10.1109/isbi.2016.7493352
The goal of longitudinal shape analysis is to understand how anatomical shape changes over time, in response to biological processes, including growth, aging, or disease. In many imaging studies, it is also critical to understand how these shape changes are affected by other factors, such as sex, disease diagnosis, IQ, etc. Current approaches to longitudinal shape analysis have focused on modeling age-related shape changes, but have not included the ability to handle covariates. In this paper, we present a novel Bayesian mixed-effects shape model that incorporates simultaneous relationships between longitudinal shape data and multiple predictors or covariates to the model. Moreover, we place an Automatic Relevance Determination (ARD) prior on the parameters, that lets us automatically select which covariates are most relevant to the model based on observed data. We evaluate our proposed model and inference procedure on a longitudinal study of Huntington's disease from PREDICT-HD. We first show the utility of the ARD prior for model selection in a univariate modeling of striatal volume, and next we apply the full high-dimensional longitudinal shape model to putamen shapes.
E. Wong, S. Palande, Bei Wang, B. Zielinski, J. Anderson, P. T. Fletcher.
“Kernel Partial Least Squares Regression for Relating Functional Brain Network Topology to Clinical Measures of Behavior,” In 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), IEEE, April, 2016.
DOI: 10.1109/isbi.2016.7493506
In this paper we present a novel method for analyzing the relationship between functional brain networks and behavioral phenotypes. Drawing from topological data analysis, we first extract topological features using persistent homology from functional brain networks that are derived from correlations in resting-state fMRI. Rather than fixing a discrete network topology by thresholding the connectivity matrix, these topological features capture the network organization across all continuous threshold values. We then propose to use a kernel partial least squares (kPLS) regression to statistically quantify the relationship between these topological features and behavior measures. The kPLS also provides an elegant way to combine multiple image features by using linear combinations of multiple kernels. In our experiments we test the ability of our proposed brain network analysis to predict autism severity from rs-fMRI. We show that combining correlations with topological features gives better prediction of autism severity than using correlations alone.
2015
M. Zhang, P. T. Fletcher.
“Finite-Dimensional Lie Algebras for Fast Diffeomorphic Image Registration,” In Information Processing in Medical Imaging (IPMI), 2015.
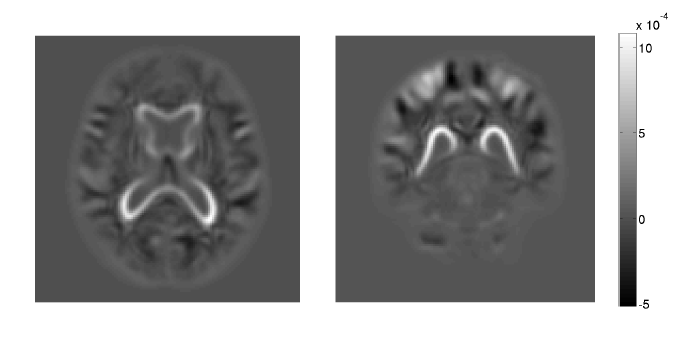
M. Zhang, P. T. Fletcher.
“Bayesian Principal Geodesic Analysis for Estimating Intrinsic Diffeomorphic Image Variability,” In Medical Image Analysis (accepted), 2015.

M. Zhang, H. Shao, P. T. Fletcher.
“A Mixture Model for Automatic Diffeomorphic Multi-Atlas Building,” In MICCAI Workshop, Springer, 2015.
Computing image atlases that are representative of a dataset
is an important first step for statistical analysis of images. Most current approaches estimate a single atlas to represent the average of a large population of images, however, a single atlas is not sufficiently expressive to capture distributions of images with multiple modes. In this paper, we present a mixture model for building diffeomorphic multi-atlases that can represent sub-populations without knowing the category of each observed data point. In our probabilistic model, we treat diffeomorphic image transformations as latent variables, and integrate them out using a Monte Carlo Expectation Maximization (MCEM) algorithm via Hamiltonian Monte Carlo (HMC) sampling. A key benefit of our model is that the mixture modeling inference procedure results in an automatic clustering of the dataset. Using 2D synthetic data generated from known parameters, we demonstrate the ability of our model to successfully recover the multi-atlas and automatically cluster the dataset. We also show the effectiveness of the proposed method in a multi-atlas estimation problem for 3D brain images.
2014
X. Hao, K. Zygmunt, R.T. Whitaker, P.T. Fletcher.
“Improved Segmentation of White Matter Tracts with Adaptive Riemannian Metrics,” In Medical Image Analysis, Vol. 18, No. 1, pp. 161--175. Jan, 2014.
DOI: 10.1016/j.media.2013.10.007
PubMed ID: 24211814

Keywords: Conformal factor, Diffusion tensor imaging, Front-propagation, Geodesic, Riemannian manifold
J. Hinkle, P.T. Fletcher, S. Joshi .
“Intrinsic Polynomials for Regression on Riemannian Manifolds,” In Journal of Mathematical Imaging and Vision, pp. 1-21. 2014.
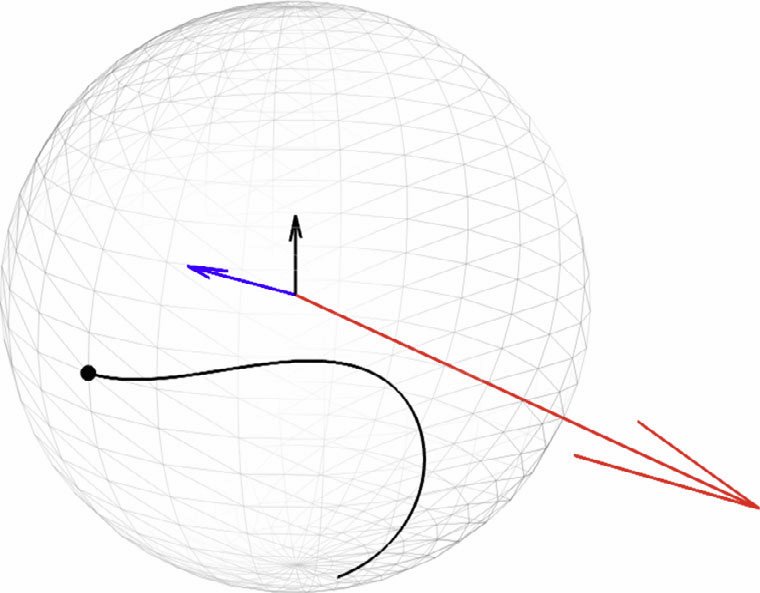
W. Liu, S.P. Awate, J.S. Anderson, P.T. Fletcher.
“A functional network estimation method of resting-state fMRI using a hierarchical Markov random field,” In NeuroImage, Vol. 100, pp. 520--534. 2014.
ISSN: 1053-8119
DOI: 10.1016/j.neuroimage.2014.06.001

Keywords: Resting-state functional MRI, Segmentation, Functional connectivity, Hierarchical Markov random field, Bayesian
P. Muralidharan, J. Fishbaugh, H.J. Johnson, S. Durrleman, J.S. Paulsen, G. Gerig, P.T. Fletcher.
“Diffeomorphic Shape Trajectories for Improved Longitudinal Segmentation and Statistics,” In Proceedings of Medical Image Computing and Computer Assisted Intervention (MICCAI), 2014.

J.A. Nielsen, B.A. Zielinski, P.T. Fletcher, A.L. Alexander, N. Lange, E.D. Bigler, J.E. Lainhart, J.S. Anderson.
“Abnormal lateralization of functional connectivity between language and default mode regions in autism,” In Molecular Autism, Vol. 5, No. 1, pp. 8. 2014.
DOI: 10.1186/2040-2392-5-8
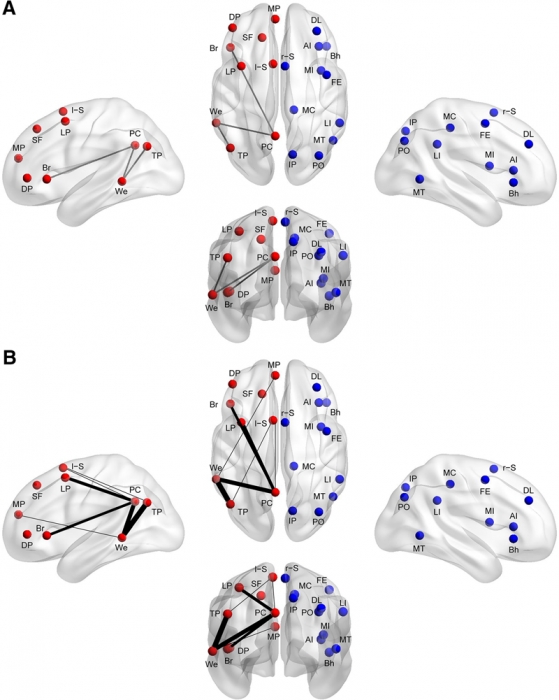
Methods: Using functional connectivity magnetic resonance imaging from a large publicly available sample (n = 964), we tested whether abnormal functional lateralization in autism exists preferentially in language regions or in a more diffuse pattern across networks of lateralized brain regions.
Results: The autism group exhibited significantly reduced left lateralization in a few connections involving language regions and regions from the default mode network, but results were not significant throughout left- and right-lateralized networks. There is a trend that suggests the lack of left lateralization in a connection involving Wernicke area and the posterior cingulate cortex associates with more severe autism.
Conclusions: Abnormal language lateralization in autism may be due to abnormal language development rather than to a deficit in hemispheric specialization of the entire brain.
Keywords: brain lateralization, brain asymmetry, autism, autism spectrum disorder, language, functional magnetic resonance imaging, functional connectivity
N. Sadeghi, P.T. Fletcher, M. Prastawa, J.H. Gilmore, G. Gerig.
“Subject-specific prediction using nonlinear population modeling: Application to early brain maturation from DTI,” In Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI 2014), 2014.
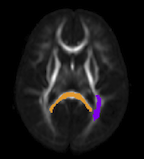
A. Sharma, P.T. Fletcher, J.H. Gilmore, M.L. Escolar, A. Gupta, M. Styner, G. Gerig.
“Parametric Regression Scheme for Distributions: Analysis of DTI Fiber Tract Diffusion Changes in Early Brain Development,” In Proceedings of the 2014 IEEE International Symposium on Biomedical Imaging (ISBI), pp. (accepted). 2014.
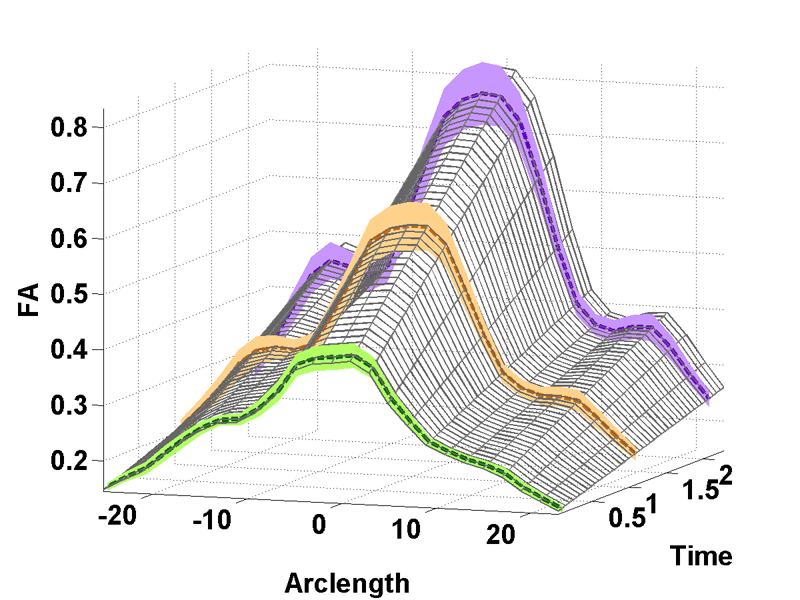
Keywords: linear regression, distribution-valued data, spatiotemporal growth trajectory, DTI, early neurodevelopment
N.P. Singh, J. Hinkle, S. Joshi, P.T. Fletcher.
“An Efficient Parallel Algorithm for Hierarchical Geodesic Models in Diffeomorphisms,” In Proceedings of the 2014 IEEE International Symposium on Biomedical Imaging (ISBI), pp. (accepted). 2014.
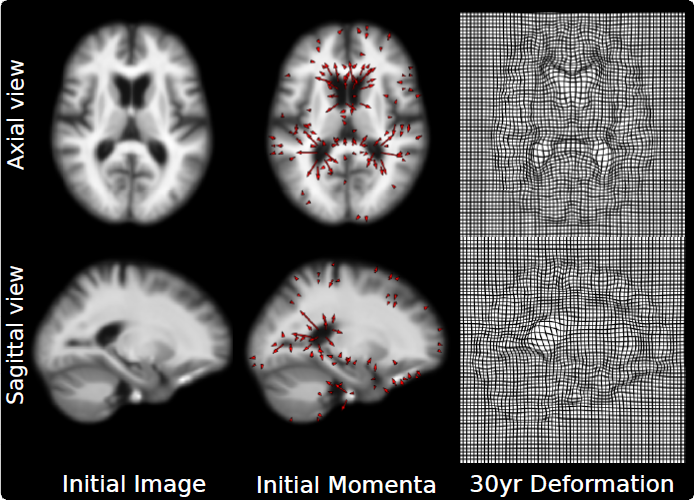
Keywords: LDDMM, HGM, Vector Momentum, Diffeomorphisms, Longitudinal Analysis
Page 1 of 6
