Bei Wang

PDF
Collaborative Research: SCALE MoDL: Advancing Theoretical Minimax Deep Learning: Optimization, Resilience, and Interpretability

Award Number and Duration

NSF DMS 2134223 (University of Utah)

NSF DMS 2134148 (University of Minnesota-Twin Cities)

September 1, 2021 to August 31, 2025 (Estimated, including 1-Year NCE)

PI and Point of Contact

Yi Zhou (PI)
Assistant Professor
Department of Electrical and Computer Engineering
University of Utah
yi.zhou AT utah.edu
Home Page

Bei Wang (co-PI)
Associate Professor
School of Computing and Scientific Computing and Imaging Institute
University of Utah
beiwang AT sci.utah.edu
Home Page

Jie Ding (PI)
Assistant Professor
School of Statistics
University of Minnesota-Twin Cities
dingj AT umn.edu
Home Page

Overview

The past decade has witnessed the great success of deep learning in broad societal and commercial applications. However, conventional deep learning relies on fitting data with neural networks, which is known to produce models that lack resilience. For instance, models used in autonomous driving are vulnerable to malicious attacks, e.g., putting an art sticker on a stop sign can cause the model to classify it as a speed limit sign; models used in facial recognition are known to be biased toward people of a certain race or gender; models in healthcare can be hacked to reconstruct the identities of patients that are used in training those models. The next-generation deep learning paradigm needs to deliver resilient models that promote robustness to malicious attacks, fairness among users, and privacy preservation. This project aims to develop a comprehensive learning theory to enhance the model resilience of deep learning. The project will produce fast algorithms and new diagnostic tools for training, enhancing, visualizing, and interpreting model resilience, all of which can have broad research and societal significance. The research activities will also generate positive educational impacts on undergraduate and graduate students. The materials developed by this project will be integrated into courses on machine learning, statistics, and data visualization and will benefit interdisciplinary students majoring in electrical and computer engineering, statistics, mathematics, and computer science. The project will actively involve underrepresented students and integrate research with education for undergraduate and graduate students in STEM. It will also produce introductory materials for K-12 students to be used in engineering summer camps.

In this project, the investigators will collaboratively develop a comprehensive minimax learning theory that advances the fundamental understanding of minimax deep learning from the perspectives of optimization, resilience, and interpretability. These complementary theoretical developments, in turn, will guide the design of novel minimax learning algorithms with substantially improved computational efficiency, statistical guarantees, and interpretability. The research includes three major thrusts. First, the investigators will develop a principled non-convex minimax optimization theory that supports scalable, fast, and convergent gradient-descent-ascent algorithms for training complex minimax deep learning models. The theory will focus on analyzing the convergence rate and sample complexity of the developed algorithms. Second, the investigators will formulate a measure of vulnerability of deep learning models and study how minimaxity can enhance their resilience against data, model, and task deviations. This theory will focus on the statistical limits of deep learning. Lastly, the investigators will establish the mathematical foundations for a set of novel visual analytics techniques that increase the model interpretability of minimax learning. In particular, the theory will provide guidance on visualizing and interpreting model resilience.

Publications and Manuscripts

Papers marked with * use alphabetic ordering of authors.
Students are underlined.

Year 3 (2023 - 2024)
	Position: Topological Deep Learning is the New Frontier for Relational Learning. Theodore Papamarkou, Tolga Birdal, Michael Bronstein, Gunnar Carlsson, Justin Curry, Yue Gao, Mustafa Hajij, Roland Kwitt, Pietro Lio, Paolo Di Lorenzo, Vasileios Maroulas, Nina Miolane, Farzana Nasrin, Karthikeyan Natesan Ramamurthy, Bastian Rieck, Simone Scardapane, Michael T. Schaub, Petar Velickovic, Bei Wang, Yusu Wang, Guo-Wei Wei, Ghada Zamzmi. Proceedings of the 41st International Conference on Machine Learning (ICML), 2024. arXiv:2402.08871
	Interpreting and generalizing deep learning in physics-based problems with functional linear models. Amirhossein Arzani, Lingxiao Yuan, Pania Newell, Bei Wang. Engineering with Computers, 2024. arXiv:2307.04569.
	In-Context Example Ordering Guided by Label Distributions. Zhichao Xu, Daniel Cohen, Bei Wang, Vivek Srikumar. Annual Conference of the North American Chapter of the Association for Computational Linguistics (NAACL), 2024. arXiv:2402.11447.
	On the Duality Gap of Constrained Cooperative Multi-Agent Reinforcement Learning. Ziyi Chen, Yi Zhou, Heng Huang. Proceedings of the 12th International Conference on Learning Representations (ICLR), 2024. OpenReview:wFWuX1Fhtj.
	Large-Scale Non-convex Stochastic Constrained Distributionally Robust Optimization. Qi Zhang, Yi Zhou, Ashley Prater-Bennette, Lixin Shen, Shaofeng Zou. Proceedings of the 38th AAAI Conference on Artificial Intelligence (AAAI), 2024. DOI: 10.1609/aaai.v38i8.28662.
	ChannelExplorer: Visual Analytics at Activation Channel's Granularity (Poster). Md Rahat-uz- Zaman, Bei Wang, Paul Rosen. IEEE Visualization Conference (IEEE VIS) Posters, 2024.
	Exploring Gradient Oscillation in Deep Neural Network Training. Chedi Morchdi, Yi Zhou, Jie Ding, Bei Wang. 59th Annual Allerton Conference on Communication, Control, and Computing (ALLERTON), 2023. Allerton 2023 Program
	Provable Identifiability of Two-Layer ReLU Neural Networks via LASSO Regularization. Gen Li, Ganghua Wang, Jie Ding. IEEE Transactions on Information Theory, 69(9), pages 5921-5935, 2023. DOI: 10.1109/TIT.2023.3274152.
	Distributed Architecture Search Over Heterogeneous Distributions. Erum Mushtaq, Chaoyang He, Jie Ding, Salman Avestimehr. Transactions on Machine Learning Research, 2023. OpenReview:sY75NqDRk1.
Year 2 (2022 - 2023)
	Visualizing and Analyzing the Topology of Neuron Activations in Deep Adversarial Training. Youjia Zhou, Yi Zhou, Jie Ding, Bei Wang. Topology, Algebra, and Geometry in Machine Learning (TAGML) Workshop at ICML, 2023. OpenReview:Q692Q3dPMe.
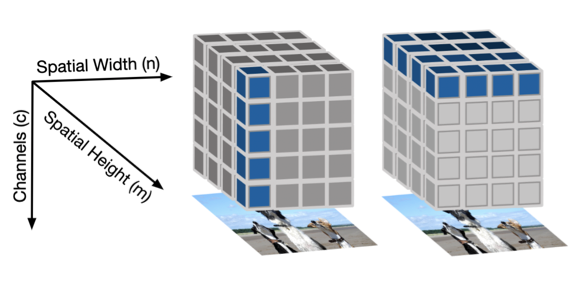
	Experimental Observations of the Topology of Convolutional Neural Network Activations. Emilie Purvine, Davis Brown, Brett Jefferson, Cliff Joslyn, Brenda Praggastis, Archit Rathore, Madelyn Shapiro, Bei Wang, Youjia Zhou. Proceedings of the 37th AAAI Conference on Artificial Intelligence (AAAI), 2023. DOI: 10.1609/aaai.v37i8.26134 arXiv:2212.00222
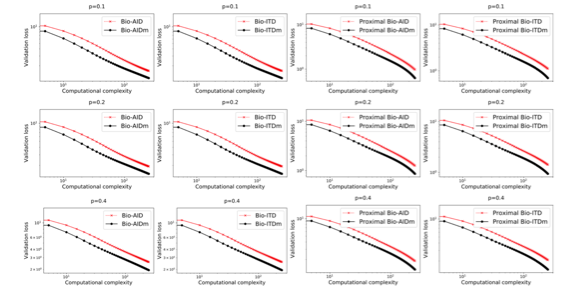
	An Accelerated Proximal Algorithm for Regularized Nonconvex and Nonsmooth Bi-level Optimization. Ziyi Chen and Bhavya Kailkhura, Yi Zhou. Machine Learning, 112(5), pages 1433-1463, 2023. DOI:10.1007/s10994-023-06329-6
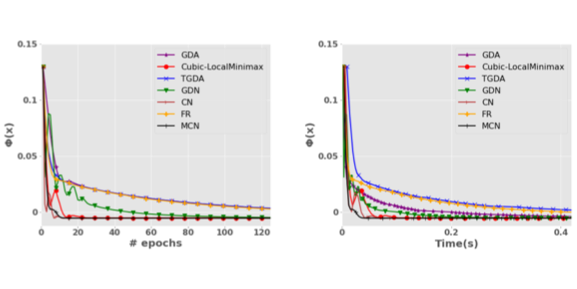
	A Cubic Regularization Approach for Finding Local Minimax Points in Nonconvex Minimax Optimization. Ziyi Chen, Zhengyang Hu, Qunwei Li, Zhe Wang, Yi Zhou. Transactions on Machine Learning Research, 2023. OpenReview:jVMMdg31De arXiv:2110.07098
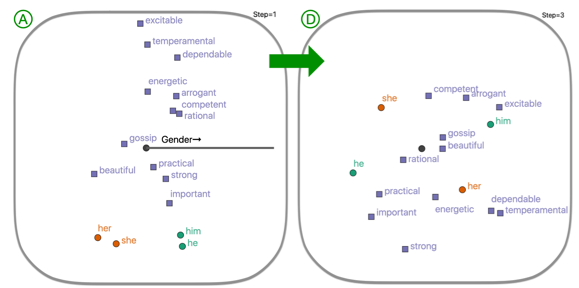
	VERB: Visualizing and Interpreting Bias Mitigation Techniques for Word Representations. Archit Rathore, Sunipa Dev, Jeff M. Phillips, Vivek Srikumar, Yan Zheng, Chin-Chia Michael Yeh, Junpeng Wang, Wei Zhang, Bei Wang. ACM Transactions on Interactive Intelligent Systems, 2023. DOI: 10.1145/3604433 arXiv:2104.02797.
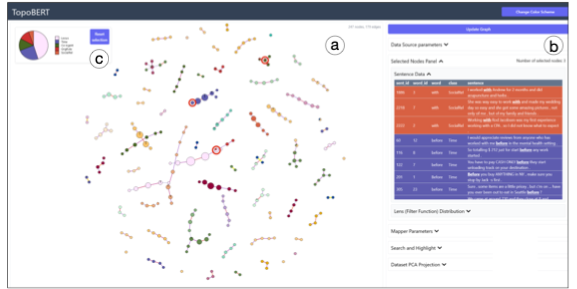
	TopoBERT: Exploring the Topology of Fine-Tuned Word Representations. Archit Rathore, Yichu Zhou, Vivek Srikumar, Bei Wang. Information Visualization, 22(3), pages 186-208, 2023. DOI: 10.1177/14738716231168671
	A Lightweight Constrained Generation Alternative for Query-focused Summarization (Short Paper). Zhichao Xu, Daniel Cohen. Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), 2023. arXiv:2304.11721
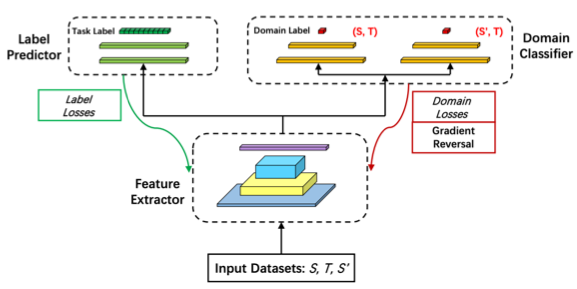
	Assisted Unsupervised Domain Adaptation. Cheng Chen, Jiawei Zhang, Jie Ding, Yi Zhou. Proceedings of the IEEE International Symposium on Information Theory (ISIT), 2023.
	Information Criteria for Model Selection. Jiawei Zhang, Yuhong Yang, Jie Ding Wiley Interdisciplinary Reviews: Computational Statistics, pages e1607, 2023.
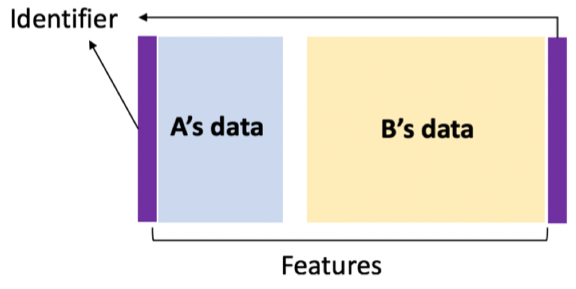
	Parallel Assisted Learning. Xinran Wang, Jiawei Zhang, Mingyi Hong, Yuhong Yang, Jie Ding. IEEE Transactions on Signal Processing, 70, pages 5848-5858, 2022.
	Finding Correlated Equilibrium of Constrained Markov Game: A Primal-Dual Approach. Ziyi Chen, Shaocong Ma, Yi Zhou. Advances in Neural Information Processing Systems (NeurIPS), 35, pages 25560-25572, 2022. Online: NeurIPS 2022 OpenReview:2-CflpDkezH
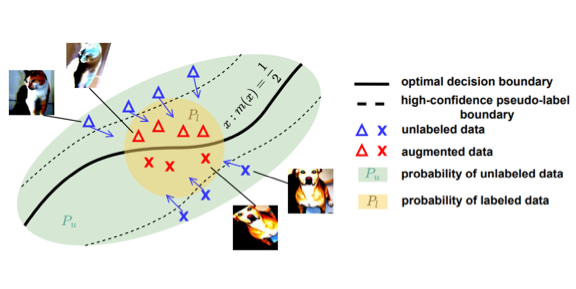
	SemiFL: Communication Efficient Semi-Supervised Federated Learning with Unlabeled Clients. Enmao Diao, Jie Ding, Vahid Tarokh. Advances in Neural Information Processing Systems (NeurIPS), 35, pages 17871-17884, 2022. Online: NeurIPS 2022 OpenReview:HUjgF0G9FxN
	The SVD of Convolutional Weights: A CNN Interpretability Framework. Brenda Praggastis, Davis Brown, Carlos Ortiz Marrero, Emilie Purvine, Madelyn Shapiro, Bei Wang. Manuscript, 2022. arXiv:2208.06894.
Year 1 (2021 - 2022)
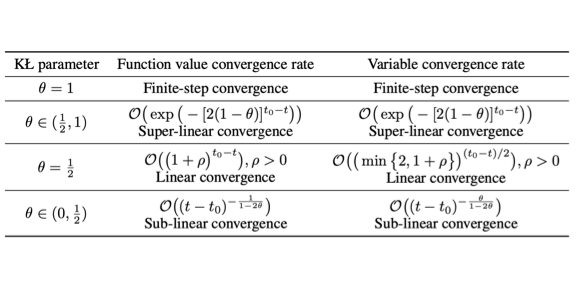
	Proximal Gradient Descent-Ascent: Variable Convergence under KL Geometry. Ziyi Chen, Yi Zhou, Tengyu Xu, Yingbin Liang. International Conference on Learning Representations (ICLR), 2021. Publisher: ICLR 2021
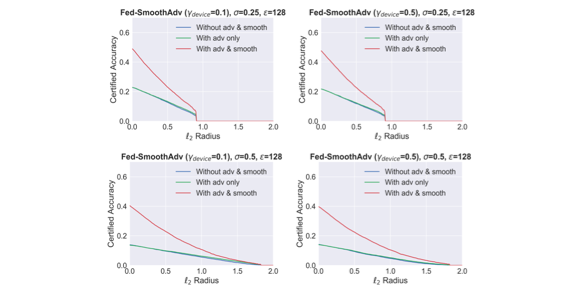
	Certifiably-Robust Federated Adversarial Learning via Randomized Smoothing. Cheng Chen, Bhavya Kailkhura, Ryan Goldhahn, Yi Zhou. IEEE 18th International Conference on Mobile Ad Hoc and Smart Systems (MASS), 2021. DOI: 10.1109/MASS52906.2021.00032
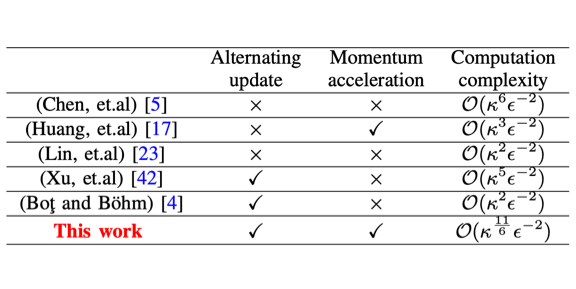
	Accelerated Proximal Alternating Gradient-Descent-Ascent for Nonconvex Minimax Machine Learning. Ziyi Chen, Shaocong Ma, Yi Zhou. IEEE International Symposium on Information Theory (ISIT), 2022.
	Sample Efficient Stochastic Policy Extragradient Algorithm for Zero-Sum Markov Game. Ziyi Chen, Shaocong Ma, Yi Zhou. International Conference on Learning Representations (ICLR), 2022. Publisher: ICLR 2022
	Mismatched Supervised Learning. Xun Xian, Mingyi Hong, Jie Ding. IEEE International Conference on Acoustics, Speech, & Signal Processing (ICASSP), 2022. DOI: 10.1109/ICASSP43922.2022.9747362
	A Framework for Understanding Model Extraction Attack and Defense. Xun Xian, Mingyi Hong, Jie Ding. Manuscript, 2022. arXiv:2206.11480

Presentations, Educational Development and Broader Impacts

Year 3 (2023 - 2024)

Bei Wang, Invited Talk, Exploring the Topology of Word Embeddings, Department of Computer Science, ETH Zurich, Institute for Visual Computing, Switzerland, July 29, 2024.
Bei Wang, Invited Talk, Topology in Data Visualization and Topology-Preserving Data Compression, Mathematical Methods in Data Science, Math Lab Talk and Discussion Series, MPI for Mathematics in the Sciences, Leipzig, Germany, June 21, 2024.

Year 2 (2022 - 2023)

Bei Wang Invited Talk, Colorado State University Topology Seminar, April 18, 2023.
Bei Wang Invited Talk, Northeastern Topology Seminar, April 11, 2023.
Bei Wang Invited Talk, Institute for Mathematical and Statistical Innovation (IMSI), Randomness in Topology and its Applications workshop, March 21, 2023.
Bei Wang Keynote Talk, Machine Learning on Higher-Order Structured data (ML-HOS) Workshop at ICDM 2022. Hypergraph Co-Optimal Transport, November 28, 2022.
Bei Wang Invited Talk, Mini Symposium on Statistics and Machine Learning in Topological and Geometric Data Analysis at SIAM Conference on Mathematics of Data Science (MDS22), September 29, 2022.

Year 1 (2021 - 2022)

Bei Wang Outreach Activity: Data Visualization with Physical Medium at Hi-GEAR Summer Camp, July 11, 2022.
Bei Wang Panelist: Applications of Topological Data Analysis to Data Science, Artificial Intelligence, and Machine Learning Workshop at SIAM International Conference on Data Mining (SDM), 2022.
Yi Zhou Tutorial Talk: Reinforcement Learning and Optimization at ICASSP 2022.
Yi Zhou Invited Talk: Assisted Learning at ITA Workshop, 2022.
Yi Zhou Tutorial Talk: Reinforcement Learning and Optimization at IEEE BigData Conference 2021.
Yi Zhou Tutorial Talk: Reinforcement Learning at ISIT 2021.
Yi Zhou Invited Talk: Minimax and Bilevel Optimization at Machine Learning Seminar series, University of Minnesota, 2021.
Yi Zhou Contributed Talk: Multi-agent Reinforcement Learning at ICML 2022.
Jie Ding Contributed Talk: Privacy-Preserving Multi-Target Multi-Domain Recommender Systems at Production and Operations Management Society Annual Conference (POMS), April 21, 2022.
Jie Ding Invited Talk: Human-Centric Privacy-Preserving Data Collection via Intervals at Department of Applied Economics and Statistics, University of Delaware, March 11, 2022.
Jie Ding Contributed Talk: Interval Privacy: A New Framework for Privacy-Preserving Data Collection at 56th Annual Conference on Information Sciences and Systems (CISS), March 9, 2022.
Jie Ding Invited Talk: Interval Privacy: A New Framework for Privacy-Preserving Data Collection at Department of Statistics and Actuarial Science, University of Iowa, Feburary 10, 2022.
Jie Ding Invited Talk: Organizational Collaboration with Assisted Learning at IMA Data Science Seminar, October 12, 2021.

Students

Current Students

Cheng Chen (ECE PhD), University of Utah

Ziyi Chen (ECE PhD), University of Utah

Weiran (Nancy) Lyu (CS PhD, Fall 2022 - present), University of Utah.

Zhichao Xu (CS PhD, Spring 2023 - present), University of Utah.

Xun Xian (ECE PhD), University of Minnesota

Jiaying Zhou (Statistics PhD), University of Minnesota

Former Students

Youjia Zhou (CS PhD, Fall 2021 - Spring 2023, graduated), University of Utah.

Archit Rathore (CS PhD, Fall 2021 - Summer 2022, graduated), University of Utah.

Khawar Murad Ahmed (CS PhD, Spring 2022, lab rotation), University of Utah.

Acknowledgement

This material is based upon work supported or partially supported by the National Science Foundation under Grant No. 2134223 and No. 2134148.

Any opinions, findings, and conclusions or recommendations expressed in this project are those of author(s) and do not necessarily reflect the views of the National Science Foundation.

Web page last update: July 3, 2023.