1. Large Scale Topological Analysis

Distributed Merge Tree Computation Algorithm for Topological Feature Extraction

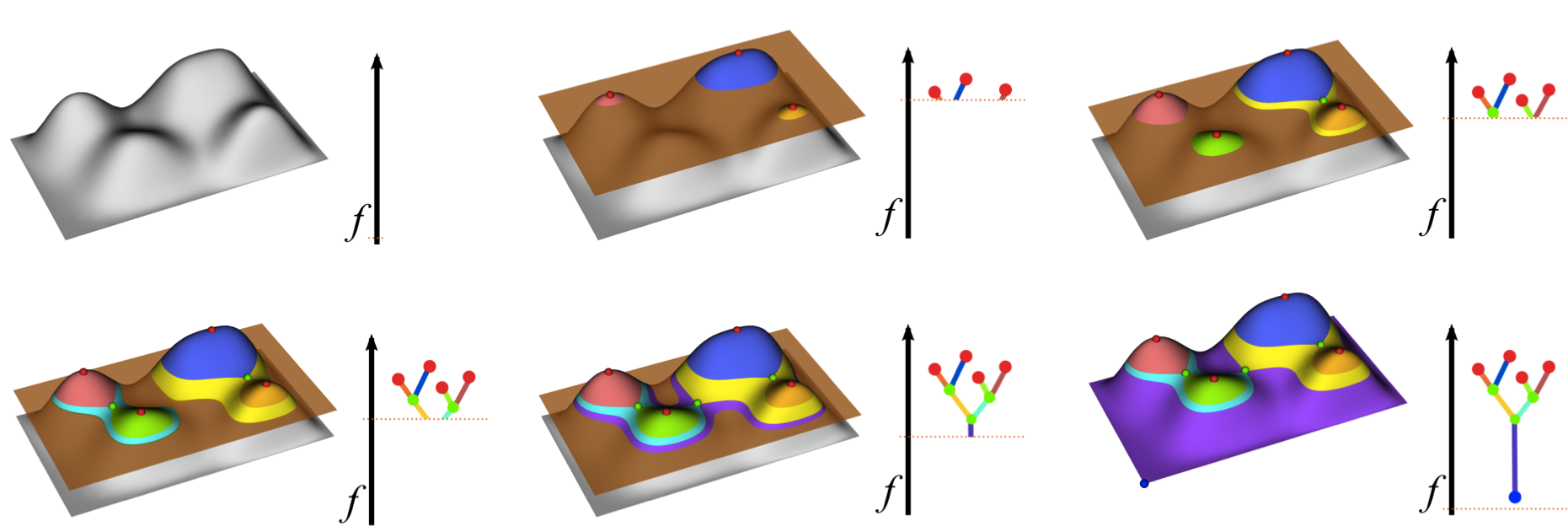
  • Project

Project Details

Collaborations

The merge tree encodes the evolution of the connected components of the super-level set of a function defined on a domain as the function range is swept from infinity to negative infinity (as shown above). The merge tree is equivalent to 0-dimensional persistence diagram. Additionally, the geometric descriptions of the super-level sets are often needed for analysis, for example, to determine volumes, shapes, track features, or for visualization. Storing the segmentation along with a merge tree enables the geometric reconstruction of super-level sets during a post-process. Furthermore, access to the segmentation at run-time allows for the pre-computation of various conditional feature-based statistics such as, for instance, average temperatures per feature. Therefore, while the merge tree itself contains only information about the number of features at each threshold, combining the merge tree with its corresponding segmentation creates a powerful and highly flexible analysis tool. We have developed a distributed algorithm for computing the merge tree on a regular CW-complex and identify the key conditions on the regular CW-complex in order to perform this computation.

Large Scale Feature Extraction of Scientific Simulations Using Segmented Merge Trees

  • Project

Project Details

Collaborations

  • Lawrence Livermore National Laboratory
  • Sandia National Laboratory
  • PDF

The ever increasing amount of data generated by scientific simulations coupled with system I/O constraints are fueling a need for analysis techniques that can extract features from the data while the simulation is running (in-situ). Of particular interest are approaches that produce reduced data representations while maintaining the ability to redefine, extract, and study features in a post-process to obtain scientific insights. Two variants of in-situ feature extraction techniques using distributed segmented merge trees are presented. The first approach is a fast, low communication cost technique that generates an exact solution but has limited scalability. The second is a scalable, local approximation that nevertheless is guaranteed to correctly extract all features up to a predefined size. We demonstrate both variants using some of the largest combustion simulations available on leadership class supercomputers at full machine scale. Our approach allows state-of-the-art, feature-based analysis to be performed in-situ at significantly higher frequency than currently possible and with negligible impact on the overall simulation runtime.

2. Visualizing Performance Metrics

BoxFish - Visualizing Network Traffic on Supercomputer Interconnects

The performance of massively parallel applications is often heavily impacted by the cost of communication among compute nodes. However, determining how to best use the network is a formidable task, made challenging by the ever increasing size and complexity of modern supercomputers. This paper applies visualization techniques to aid parallel application developers in understanding the network activity by enabling a detailed exploration of the flow of packets through the hardware interconnect. In order to visualize this large and complex data, we employ two linked views of the hardware network. The first is a 2D view, that represents the network structure as one of several simplified planar projections. This view is designed to allow a user to easily identify trends and patterns in the network traffic. The second is a 3D view that augments the 2D view by preserving the physical network topology and providing a context that is familiar to the application developers. Using the massively parallel multi-physics code pF3D as a case study, we demonstrate that our tool provides valuable insight that we use to explain and optimize pF3D's performance on an IBM Blue Gene/P system.

Project Details

Collaborations

Interactive Linked Visualization for Performance Analysis of Heterogenous Clusters

  • Project

Performance data obtained from compute clusters is necessarily complicated because data is not just collected from a single node but from multiple interacting nodes, potentially with several cores each. Further, heterogeneous clusters, often in the form of nodes combining one ore more CPUs working together with several GPUs, are becoming more commonplace and are leading to even more complexity. These characteristics pose a serious challenge to the analysis and improvement of application performance. We present a tool that assists performance analysis by visualizing performance data with the help of various linked views that: 1) Draw correlations between the domain decomposition of the application and collected performance data; 2) Enable views of the data at various granularities within the appropriate context; 3) Provide a combined visualization of performance data from the CPUs as well as GPUs; and 4) Increase the intuition behind the analysis of performance data.

Project Details

Collaborations

  • Lawrence Livermore National Laboratory
  • University of California ,Davis
  • Clemson University
    • PDF

3. Course Work Projects

Machine Learning : Scalable Domain Adaptation via Intelligent Sampling

  • Project

In the area of deploying machine learning systems, Domain Adaptation is an important task which we encounter in real world. Here the goal is to build our model based on some fixed source domain and then deploy it to one or more different target domains. In many applications, it is expensive and time consuming to collect labeled training samples. On the other side, classifiers trained with only a limited number of labeled patterns are usually not robust. In practice, the computational cost for domain adaptation will grow fast as the data sets become larger and more unlabelled data is cheaply available. In this paper, we consider a semi-supervised domain adaptation technique named DTMKL(Domain Transfer Multiple Kernel Learning) which can learn robust classifiers with only a limited number of labeled patterns from the target domain by leveraging a large amount of labeled training data from other auxiliary(which we call source) domains. Under the framework of DTMKL, we propose an approach based on intelligent sampling on the unlabeled data which achieves a 3x speedup in training time with less than 1% reduction in accuracy.

Project Details

Collaborations