SCI Publications
2021
M. Højgaard Jensen, L. Hilgendorf, S. Joshi, S. Sommer.
“Bridge Simulation on Lie Groups and Homogeneous Spaces with Application to Parameter Estimation,” Subtitled “arXiv:2112.00866,” 2021.
L. Kühnel, T. Fletcher, S. Joshi, S. Sommer.
“Latent Space Geometric Statistics,” In Pattern Recognition. ICPR International Workshops and Challenges: Virtual Event, January 10–15, 2021, Proceedings, Part VI, Springer International Publishing, pp. 163-178. 2021.
Deep generative models, e.g., variational autoencoders and generative adversarial networks, result in latent representation of observed data. The low dimensionality of the latent space provides an ideal setting for analysing high-dimensional data that would otherwise often be infeasible to handle statistically. The linear Euclidean geometry of the high-dimensional data space pulls back to a nonlinear Riemannian geometry on latent space where classical linear statistical techniques are no longer applicable. We show how analysis of data in their latent space representation can be performed using techniques from the field of geometric statistics. Geometric statistics provide generalisations of Euclidean statistical notions including means, principal component analysis, and maximum likelihood estimation of parametric distributions. Introduction to estimation procedures on latent space are considered, and the …
A. Singh, M. Bauer, S. Joshi.
“Physics Informed Convex Artificial Neural Networks (PICANNs) for Optimal Transport based Density Estimation,” Subtitled “arXiv,” 2021.
Optimal Mass Transport (OMT) is a well studied problem with a variety of applications in a diverse set of fields ranging from Physics to Computer Vision and in particular Statistics and Data Science. Since the original formulation of Monge in 1781 significant theoretical progress been made on the existence, uniqueness and properties of the optimal transport maps. The actual numerical computation of the transport maps, particularly in high dimensions, remains a challenging problem. By Brenier's theorem, the continuous OMT problem can be reduced to that of solving a non-linear PDE of Monge-Ampere type whose solution is a convex function. In this paper, building on recent developments of input convex neural networks and physics informed neural networks for solving PDE's, we propose a Deep Learning approach to solve the continuous OMT problem.
To demonstrate the versatility of our framework we focus on the ubiquitous density estimation and generative modeling tasks in statistics and machine learning. Finally as an example we show how our framework can be incorporated with an autoencoder to estimate an effective probabilistic generative model.
2018
O. Abdullah, L. Dai, J. Tippetts, B. Zimmerman, A. Van Hoek, S. Joshi, E. Hsu.
“High resolution and high field diffusion MRI in the visual system of primates (P3.086),” In Neurology, Vol. 90, No. 15 Supplement, Wolters Kluwer Health, Inc, 2018.
ISSN: 0028-3878
Objective: Establishing a primate multiscale genetic brain network linking key microstructural brain components to social behavior remains an elusive goal.
Background: Diffusion MRI, which quantifies the magnitude and anisotropy of water diffusion in brain tissues, offers unparalleled opportunity to link the macroconnectome (resolution of ~0.5mm) to histological-based microconnectome at synaptic resolution.
Design/Methods: We tested the hypothesis that the simplest (and most clinically-used) reconstruction technique (known as diffusion tensor imaging, DTI) will yield similar brain connectivity patterns in the visual system (from optic chiasm to visual cortex) compared to more sophisticated and accurate reconstruction methods including diffusion spectrum imaging (DSI), q-ball imaging (QBI), and generalized q-sampling imaging. We obtained high resolution diffusion MRI data on ex vivo brain from Macaca fascicularis: MRI 7T, resolution 0.5 mm isotropic, 515 diffusion volumes up to b-value (aka diffusion sensitivity) of 40,000 s/mm2 with scan time ~100 hrs.
Results: Tractography results show that despite the limited ability of DTI to resolve crossing fibers at the optic chiasm, DTI-based tracts mapped to the known projections of layers in lateral geniculate nucleus and to the primary visual cortex. The other reconstructions were superior in localized regions for resolving crossing regions.
Conclusions: In conclusion, despite its simplifying assumptions, DTI-based fiber tractography can be used to generate accurate brain connectivity maps that conform to established neuroanatomical features in the visual system.
M.D. Foote, B. Zimmerman, A. Sawant, S. Joshi.
“Real-Time Patient-Specific Lung Radiotherapy Targeting using Deep Learning,” In 1st Conference on Medical Imaging with Deep Learning (MIDL 2018), Amsterdam, The Netherlands, 2018.
Radiation therapy has presented a need for dynamic tracking of a target tumor volume. Fiducial markers such as implanted gold seeds have been used to gate radiation delivery but the markers are invasive and gating significantly increases treatment time. Pretreatment acquisition of a 4DCT allows for the development of accurate motion estimation for treatment planning. A deep convolutional neural network and subspace motion tracking is used to recover anatomical positions from a single radiograph projection in real-time. We approximate the nonlinear inverse of a diffeomorphic transformation composed with radiographic projection as a deep network that produces subspace coordinates to define the patient-specific deformation of the lungs from a baseline anatomic position. The geometric accuracy of the subspace projections on real patient data is similar to accuracy attained by original image registration between individual respiratory-phase image volumes.
L. Kuhnel, T. Fletcher, S. Joshi, S. Sommer.
“Latent Space Non-Linear Statistics,” In CoRR, 2018.
Given data, deep generative models, such as variational autoencoders (VAE) and generative adversarial networks (GAN), train a lower dimensional latent representation of the data space. The linear Euclidean geometry of data space pulls back to a nonlinear Riemannian geometry on the latent space. The latent space thus provides a low-dimensional nonlinear representation of data and classical linear statistical techniques are no longer applicable. In this paper we show how statistics of data in their latent space representation can be performed using techniques from the field of nonlinear manifold statistics. Nonlinear manifold statistics provide generalizations of Euclidean statistical notions including means, principal component analysis, and maximum likelihood fits of parametric probability distributions. We develop new techniques for maximum likelihood inference in latent space, and adress the computational complexity of using geometric algorithms with high-dimensional data by training a separate neural network to approximate the Riemannian metric and cometric tensor capturing the shape of the learned data manifold.
2017
M. Foote, P. Sabouri, A. Sawant, S. Joshi.
“Rank Constrained Diffeomorphic Density Motion Estimation for Respiratory Correlated Computed Tomography,” In Graphs in Biomedical Image Analysis, Computational Anatomy and Imaging Genetics, Springer International Publishing, pp. 177--185. 2017.
DOI: 10.1007/978-3-319-67675-3_16
Motion estimation of organs in a sequence of images is important in numerous medical imaging applications. The focus of this paper is the analysis of 4D Respiratory Correlated Computed Tomography (RCCT) Imaging. It is hypothesized that the quasi-periodic breathing induced motion of organs in the thorax can be represented by deformations spanning a very low dimension subspace of the full infinite dimensional space of diffeomorphic transformations. This paper presents a novel motion estimation algorithm that includes the constraint for low-rank motion between the different phases of the RCCT images. Low-rank deformation solutions are necessary for the efficient statistical analysis and improved treatment planning and delivery. Although the application focus of this paper is RCCT the algorithm is quite general and applicable to various motion estimation problems in medical imaging.
2014
S. Durrleman, M. Prastawa, N. Charon, J.R. Korenberg, S. Joshi, G. Gerig, A. Trouvé.
“Morphometry of anatomical shape complexes with dense deformations and sparse parameters,” In NeuroImage, 2014.
DOI: 10.1016/j.neuroimage.2014.06.043
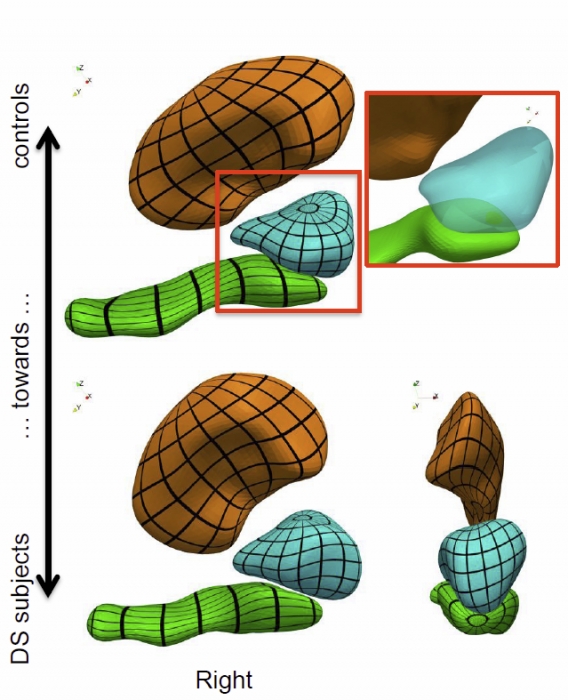
We propose a generic method for the statistical analysis of collections of anatomical shape complexes, namely sets of surfaces that were previously segmented and labeled in a group of subjects. The method estimates an anatomical model, the template complex, that is representative of the population under study. Its shape reflects anatomical invariants within the dataset. In addition, the method automatically places control points near the most variable parts of the template complex. Vectors attached to these points are parameters of deformations of the ambient 3D space. These deformations warp the template to each subject’s complex in a way that preserves the organization of the anatomical structures. Multivariate statistical analysis is applied to these deformation parameters to test for group differences. Results of the statistical analysis are then expressed in terms of deformation patterns of the template complex, and can be visualized and interpreted.
The user needs only to specify the topology of the template complex and the number of control points. The method then automatically estimates the shape of the template complex, the optimal position of control points and deformation parameters. The proposed approach is completely generic with respect to any type of application and well adapted to efficient use in clinical studies, in that it does not require point correspondence across surfaces and is robust to mesh imperfections such as holes, spikes, inconsistent orientation or irregular meshing.
The approach is illustrated with a neuroimaging study of Down syndrome (DS). Results demonstrate that the complex of deep brain structures shows a statistically significant shape difference between control and DS subjects. The deformation-based modelingis able to classify subjects with very high specificity and sensitivity, thus showing important generalization capability even given a low sample size. We show that results remain significant even if the number of control points, and hence the dimension of variables in the statistical model, are drastically reduced. The analysis may even suggest that parsimonious models have an increased statistical performance.
The method has been implemented in the software Deformetrica, which is publicly available at www.deformetrica.org.
Keywords: morphometry, deformation, varifold, anatomy, shape, statistics
J. Hinkle, P.T. Fletcher, S. Joshi .
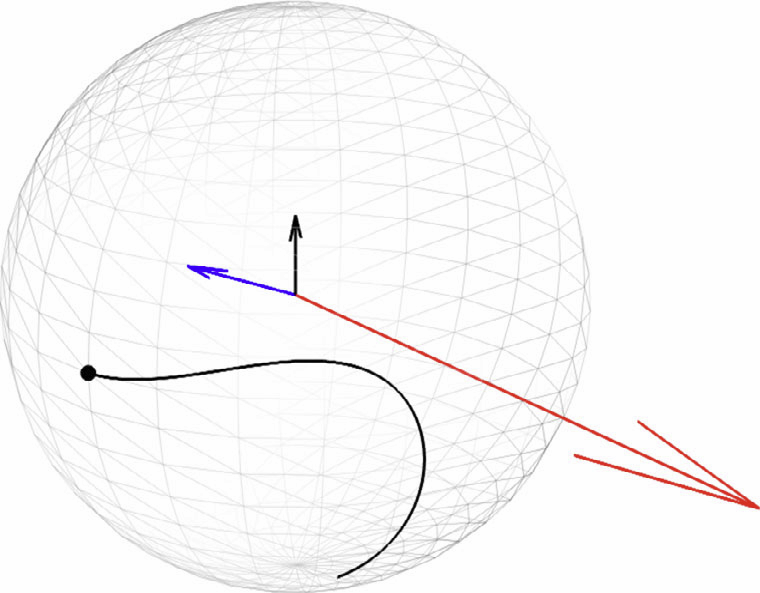
“Intrinsic Polynomials for Regression on Riemannian Manifolds,” In Journal of Mathematical Imaging and Vision, pp. 1-21. 2014.
N.P. Singh, J. Hinkle, S. Joshi, P.T. Fletcher.
“An Efficient Parallel Algorithm for Hierarchical Geodesic Models in Diffeomorphisms,” In Proceedings of the 2014 IEEE International Symposium on Biomedical Imaging (ISBI), pp. (accepted). 2014.
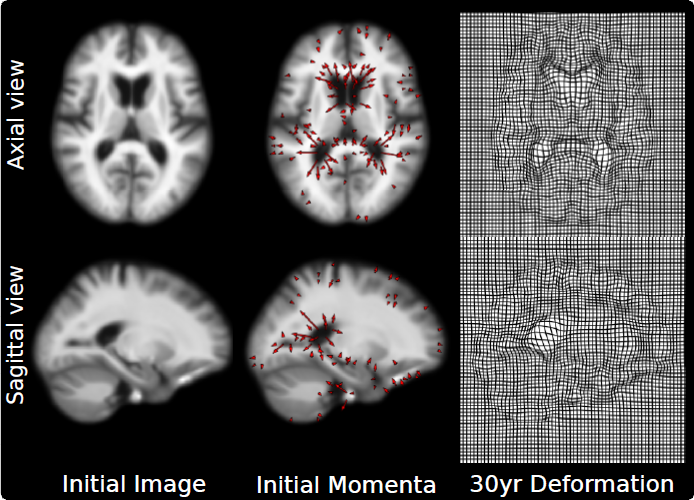
Keywords: LDDMM, HGM, Vector Momentum, Diffeomorphisms, Longitudinal Analysis
2013
S. Durrleman, S. Allassonnière, S. Joshi.
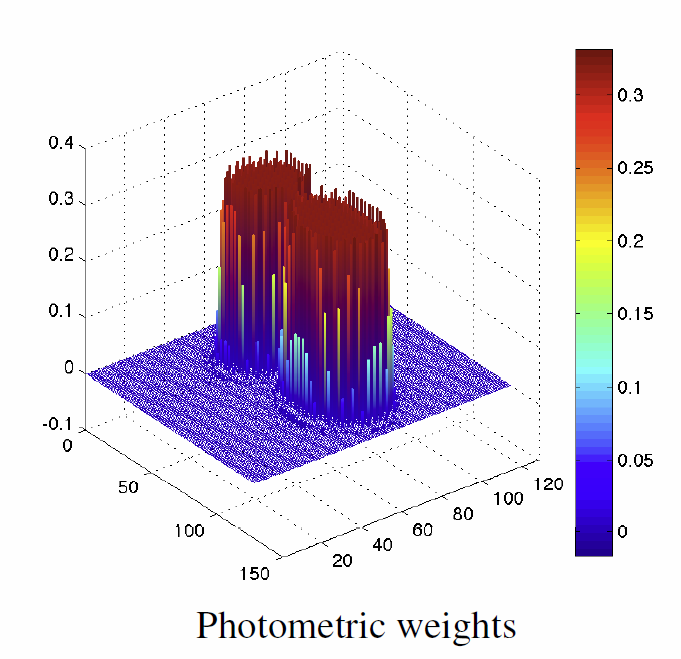
“Sparse adaptive parameterization of variability in image ensembles,” In International Journal of Computer Vision (IJCV), Vol. 101, No. 1, pp. 161--183. 2013.
DOI: 10.1007/s11263-012-0556-1
J. Hinkle, S. Joshi.
“PDiff: Irrotational Diffeomorphisms for Computational Anatomy,” In Proceedings of the International Conference on Information Processing in Medical Imaging (IPMI), Lecture Notes in Computer Science (LNCS), pp. (accepted). 2013.
N.P. Singh, J. Hinkle, S. Joshi, P.T. Fletcher.
“A Vector Momenta Formulation of Diffeomorphisms for Improved Geodesic Regression and Atlas Construction,” In Proceedings of the 2013 IEEE 10th International Symposium on Biomedical Imaging (ISBI), Note: Received Best Student Paper Award, pp. 1219--1222. 2013.
DOI: 10.1109/ISBI.2013.6556700

Keywords: LDDMM, Geodesic regression, Atlas, Vector Momentum
N.P. Singh, J. Hinkle, S. Joshi, P.T. Fletcher.
“A Hierarchical Geodesic Model for Diffeomorphic Longitudinal Shape Analysis,” In Proceedings of the International Conference on Information Processing in Medical Imaging (IPMI), Lecture Notes in Computer Science (LNCS), pp. (accepted). 2013.
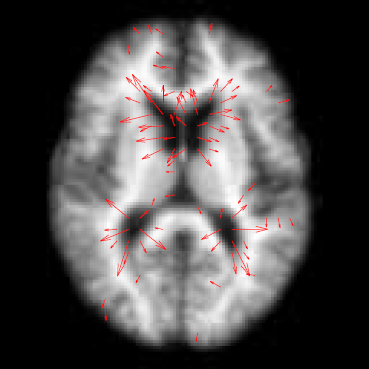
M. Szegedi, J. Hinkle, P. Rassiah, V. Sarkar, B. Wang, S. Joshi, B. Salter.
“Four‐dimensional tissue deformation reconstruction (4D TDR) validation using a real tissue phantom,” In Journal of Applied Clinical Medical Physics, Vol. 14, No. 1, pp. 115-132. 2013.
DOI: 10.1120/jacmp.v14i1.4012
Calculation of four‐dimensional (4D) dose distributions requires the remapping of dose calculated on each available binned phase of the 4D CT onto a reference phase for summation. Deformable image registration (DIR) is usually used for this task, but unfortunately almost always considers only endpoints rather than the whole motion path. A new algorithm, 4D tissue deformation reconstruction (4D TDR), that uses either CT projection data or all available 4D CT images to reconstruct 4D motion data, was developed. The purpose of this work is to verify the accuracy of the fit of this new algorithm using a realistic tissue phantom. A previously described fresh tissue phantom with implanted electromagnetic tracking (EMT) fiducials was used for this experiment. The phantom was animated using a sinusoidal and a real patient‐breathing signal. Four‐dimensional computer tomography (4D CT) and EMT tracking were performed. Deformation reconstruction was conducted using the 4D TDR and a modified 4D TDR which takes real tissue hysteresis (4D TDRHysteresis) into account. Deformation estimation results were compared to the EMT and 4D CT coordinate measurements. To eliminate the possibility of the high contrast markers driving the 4D TDR, a comparison was made using the original 4D CT data and data in which the fiducials were electronically masked. For the sinusoidal animation, the average deviation of the 4D TDR compared to the manually determined coordinates from 4D CT data was 1.9 mm, albeit with as large as 4.5 mm deviation. The 4D TDR calculation traces matched 95% of the EMT trace within 2.8 mm. The motion hysteresis generated by real tissue is not properly projected other than at endpoints of motion. Sinusoidal animation resulted in 95% of EMT measured locations to be within less than 1.2 mm of the measured 4D CT motion path, enabling accurate motion characterization of the tissue hysteresis. The 4D TDRHysteresis calculation traces accounted well for the hysteresis and matched 95% of the EMT trace within 1.6 mm. An irregular (in amplitude and frequency) recorded patient trace applied to the same tissue resulted in 95% of the EMT trace points within less than 4.5 mm when compared to both the 4D CT and 4D TDRHysteresis motion paths. The average deviation of 4D TDRHysteresis compared to 4D CT datasets was 0.9 mm under regular sinusoidal and 1.0 mm under irregular patient trace animation. The EMT trace data fit to the 4D TDRHysteresis was within 1.6 mm for sinusoidal and 4.5 mm for patient trace animation. While various algorithms have been validated for end‐to‐end accuracy, one can only be fully confident in the performance of a predictive algorithm if one looks at data along the full motion path. The 4D TDR, calculating the whole motion path rather than only phase‐ or endpoints, allows us to fully characterize the accuracy of a predictive algorithm, minimizing assumptions. This algorithm went one step further by allowing for the inclusion of tissue hysteresis effects, a real‐world effect that is neglected when endpoint‐only validation is performed. Our results show that the 4D TDRHysteresis correctly models the deformation at the endpoints and any intermediate points along the motion path.
PACS numbers: 87.55.km, 87.55.Qr, 87.57.nf, 87.85.Tu
2012
S. Durrleman, M.W. Prastawa, S. Joshi, G. Gerig, A. Trouve.
“Topology Preserving Atlas Construction from Shape Data without Correspondence using Sparse Parameters,” In Proceedings of MICCAI 2012, Lecture Notes in Computer Science (LNCS), pp. 223--230. October, 2012.
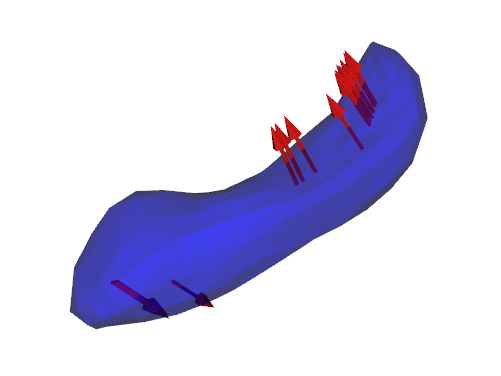
S. Durrleman, S. Allassonniere, S. Joshi.
“Sparse Adaptive Parameterization of Variability in Image Ensembles,” In International Journal of Computer Vision, pp. 1--23. 2012.
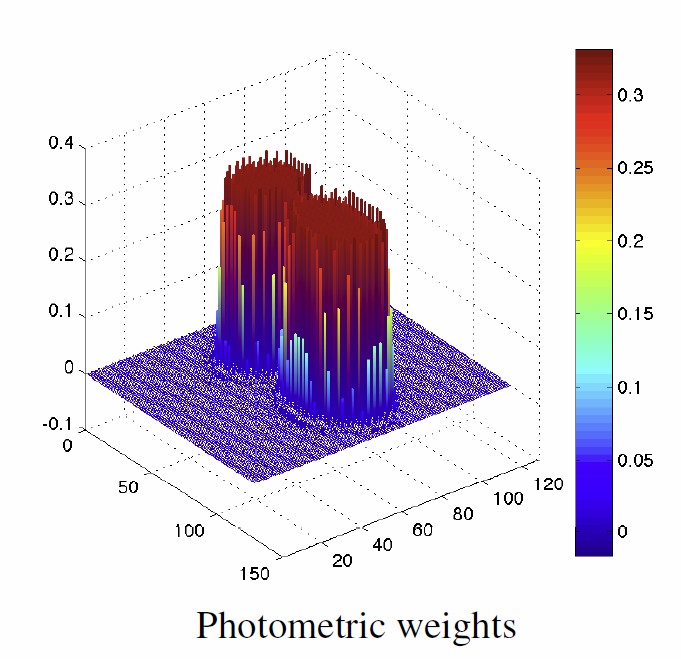
L.K. Ha, J. Krüger, J.L.D. Comba, C.T. Silva, S. Joshi.
“ISP: An Optimal Out-of-Core Image-Set Processing Streaming Architecture for Parallel Heterogeneous Systems,” In IEEE Transactions on Visualization and Computer Graphics (TVCG), Vol. 18, No. 6, pp. 838--851. 2012.
DOI: 10.1109/TVCG.2012.32
Image population analysis is the class of statistical methods that plays a central role in understanding the development, evolution and disease of a population. However, these techniques often require excessive computational power and memory that are compounded with a large number of volumetric inputs. Restricted access to supercomputing power limits its influence in general research and practical applications. In this paper we introduce ISP, an Image-Set Processing streaming framework that harnesses the processing power of commodity heterogeneous CPU/GPU systems and attempts to solve this computational problem. In ISP we introduce specially-designed streaming algorithms and data structures that provide an optimal solution for out-of-core multi-image processing problems both in terms of memory usage and computational efficiency. ISP makes use of the asynchronous execution mechanism supported by parallel heterogeneous systems to efficiently hide the inherent latency of the processing pipeline of out-of-core approaches. Consequently, with computationally intensive problems, the ISP out-of-core solution can achieve the same performance as the in-core solution. We demonstrate the efficiency of the ISP framework on synthetic and real datasets.
L.K. Ha, J. Krüger, J.L.D. Comba, C.T. Silva, S. Joshi.
“ISP: An Optimal Out-of-Core Image-Set Processing Streaming Architecture for Parallel Heterogeneous Systems,” In IEEE Transactions on Visualization and Computer Graphics, Vol. 18, No. 5, pp. 838--851. 2012.
DOI: 10.1109/TVCG.2012.32
J. Hinkle, P. Muralidharan, P.T. Fletcher, S. Joshi.
“Polynomial Regression on Riemannian Manifolds,” In arXiv, Vol. 1201.2395, 2012.

Page 2 of 7
