In many visual classification tasks, it is easy for a human to classify the training samples perfectly; however, the decision boundary is highly nonlinear in the space of pixel intensities. Therefore, we can argue that, the data corresponding to every class lies on a highly nonlinear manifold in the high dimensional space of pixel intensities and these manifolds don’t intersect with each other. An optimal decision boundary lies between the manifolds of different classes where there are no or very few samples. Decision boundaries can be pushed away from training samples by maximizing their margin. Furthermore, it is not necessary to know the class labels of the samples to maximize the margin of a classifier as in TSVMs. However, finding a classifier with a large margin is only possible if the feature set is chosen or found appropriately. For TSVMs the burden is on the kernel of choice. On the other hand, since ConvNets are feature generators without their final fully connected classification layer, if there is a feature space that allows a large margin classifier, they should be capable of finding it in theory. Our argument then is that since object recognition is a relatively easy task for a human, there must be such a feature space that ConvNets can generate with a large margin. Motivated by this argument, we propose a regularization term that uses unlabeled data to encourage the classification layer of a ConvNet to have a large margin. In other words, we propose a regularization term which makes use of unlabeled data and pushes the decision boundary to a less dense area of decision space and forces the set of predictions for a multiclass dataset to be mutually-exclusive. Here is the unsupervised loss function that we minimize:

$$ l_{\cal U}(\mathbf{f}(\mathbf{w}, \mathbf{x}_i)) = -\sum_{j=1}^{K} f_j(\mathbf{w},\mathbf{x}_i) \prod_{k=1,\, k\neq j}^{K} (1-f_k(\mathbf{w},\mathbf{x}_i)) $$

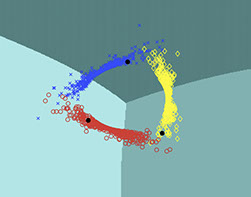
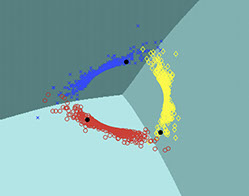
Here, \( \mathbf{f}(\mathbf{w}, \mathbf{x}) \) is the output vector of a general classifier with learning parameters \( \mathbf{w} \) and input vector \( \mathbf{x} \). \( K \) is the number of classes. The following figures show a synthetic dataset with three classes of diamonds, circles and crosses. Labeled samples are shown with black circles. We trained a simple two layer neural network on this dataset. The figure on the left is trained without our unsupervised loss function and the figure on the right is trained using our loss function. We can see that our unsupervised loss guides the decision boundaries to the right places.

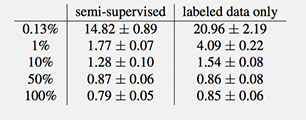
We evaluated our model on MNIST, CIFAR10, NORB and SVHN datasets. We also show some preliminary results on ILSVRC 2012 using AlexNet model. In separate experiments, we randomly pick 1%, 10%, 50% and 100% of training data as labeled set and the rest is reserved for unlabeled set.

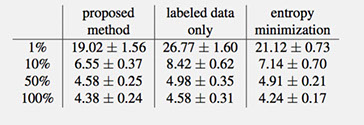
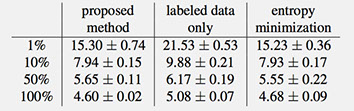
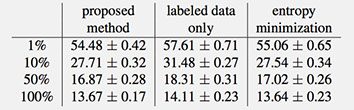
We performed preliminary experiments with ILSVRC 2012 which has 1000 classes. We randomly picked 10% of each class from training data as labeled set and the rest was used for unlabeled set. We applied our regularization term to AlexNet model. Using our method we achieved an error rate of 42.90%. If we don’t use the regularization term the error rate is 45.63%.

References:

[1] Mehdi Sajjadi, Mehran Javanmardi, and Tolga Tasdizen. "Mutual exclusivity loss for semi-supervised deep learning." 2016 IEEE International Conference on Image Processing (ICIP). IEEE, 2016.

[2] Grandvalet, Yves, and Yoshua Bengio. "Semi-supervised learning by entropy minimization." Advances in neural information processing systems. 2004.