Introduction
Research projects in our group range from general classification and regression algorithms to high level image understanding with diverse applications in biomedical images. Here, we present our works on three research topics. We describe Disjunctive Normal Networks (DNN) which are the basis for our classification, regression and shape modeling algorithms. Combination of DNNs and Cascaded Hierarchical Models (CHM) provides a state-of-the-art scene labeling framework that can be used to produce probability maps for segmentation of Electron Microscopy (EM) images. Hierarchical Merge Trees (HMT) use the output of CHM and produce accurate region segmentation for EM data which is the primary step for creating a connectome. We also present our works on Semi-Supervised Learning (SSL) which exploits unlabeled data to improve the accuracy of a classifier.
Logistic Disjunctive Normal Network (LDNN) is a general binary classifier that is designed to find the classification function in disjunctive normal form. LDNN achieves state-of-the-art results on general classification problems. LDNN is a flexible and promising learning structure that can be used in a variety of frameworks for different machine learning tasks including but not limited to regression, object recognition, scene labeling and shape modeling.
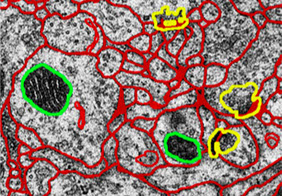
Accurate segmentation of individual neuron cells in electron microscopy (EM) images is very important to quantitative connectomics research. EM images are typically hard to segment. The first step for EM segmentation is automatically detecting cell membranes using supervised machine learning, which results in probability maps of cell boundaries. Then region segmentation is generated that assigns each neuron cell a unique integer label.
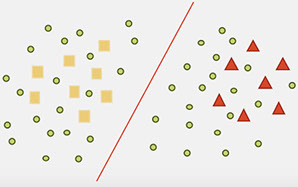
Training high accuracy classifiers often requires a very large amount of labeled training data. Unfortunately, building large labeled datasets is a costly and time consuming process. On the other hand, unlabeled data is easy to obtain. Semi-supervised learning (SSL) uses unlabeled data to train a model with higher accuracy when there is a limited set of labeled data available. The following example illustrates the effect of unlabeled data on decision function.
© 2014
Scientific Computing and Imaging Institute