Disjunctive Normal Shape Model (DNSM) is a differentiable implicit and parametric shape model where the parameters of the model are the angles and positions of linear discriminants which form the boundary of the shape. DNSM is formed as a union of \( N \) polytopes which themselves are created by intersections of \( M \) discriminant half-spaces. The differentiable approximation of the characteristic function \( \hat{f} (\mathbf{x}) \) of the DNSM is given as

$$ \hat{f}(\mathbf{x};\mathbf{W}) = 1 - \prod _{i=1}^N \left(1-  \underbrace{\prod_{j=1}^M \frac{1}{1+e^{-\sum_{k=1}^n w_{ijk}x_k+b_{ij}}}}_{g_i(\mathbf{x})}\right), $$

where \(\mathbf{x} =\{x,y,1\}\) for two-dimensional (2D) shapes and \(\mathbf{x} = \{x,y,z,1\}\) for three-dimensional (3D) shapes. The only adaptive parameters are the weights \(w_{ijk}\) and biases \(b_{ij}\) of the sigmoid functions \(\sigma_{ij}(\mathbf{x})\) which define the orientations and positions of the linear discriminants that form the shape boundary. The conjunctions of \(\sigma_{ij}(\mathbf{x})\) form the convex polytope \(g_i(\mathbf{x})\). \(\hat{f}(\mathbf{x}):\mathbf{R}^D\rightarrow [0,1]\), and the level set \(\hat{f}(\mathbf{x}) = 0.5\) represents the interface between the foreground \(\hat{f}(\mathbf{x})>0.5\) (inside the shape) and background \(\hat{f}(\mathbf{x})<0.5\) regions.

The DNSM formulation in above equation can also be used as a parametric level set by making two modifications. First, instead of using the application domain knowledge to decide on the small number of polytopes needed, we can use a large number of polytopes, \(N\), in the DNSM formulation, and initialize the level set with regularly distributed polytopes. Second, for computational efficiency, we can use only the neighboring polytopes, \(\aleph (\mathbf{x})\), for each location, \(\mathbf{x}\), in the image.

The goal of DNSM-based segmentation can be formulated as the estimation of the optimal DNSM parameters, \(\mathbf{W}=\{w_{ijk}\}\), given an image \(I:\Omega\rightarrow R\). In the Bayesian framework, this can be computed by maximizing the posterior distribution \( \mathcal P(\mathbf{W}/I) \propto \mathcal P(I/\mathbf{W}) \mathcal P(\mathbf{W}) \). The most probable segmentation of a given image is then obtained by maximizing the posterior probability, which is equivalent to minimizing its negative logarithm. Therefore the energy to be minimized is given as

$$ E(\mathbf{W}) =  - \log \mathcal P(I/\mathbf{W}) - \log \mathcal P(\mathbf{W}) $$

where the first term is an image-based term which depends on the observation \( I \) that can consist of features such as intensity, color and texture. The second term is based on geometry, and it can be used to introduce prior shape knowledge. When there are training samples available, we model the appearance \( \mathcal P(I/\mathbf{W}) \) and shape \( \mathcal P(\mathbf{W}) \) using nonparametric kernel density estimation on the discriminant parameter space. DNSM allows the use of powerful local prior statistics at any scale in a Bayesian inference framework. When using the DNSM as a level set without any training data set, \( \mathcal P(I/\mathbf{W}) \) can represent a region based data term, and the energy to be minimized can be given as \( E(\mathbf{W}) =  \sum_{r=1}^R \int_{\Omega_r} - \log \mathcal P_r(I(\mathbf{x}), \mathbf{x})\mathbf{dx} - \log \mathcal P(\mathbf{W}) \), where \( \mathcal P_r \) is the probability density of region \( r \). Therefore, we can use DNSM for the segmentation of both two-phase (\( R=2 \)) and multiphase (\( R>2 \)) cases.

 

Experiments:

 

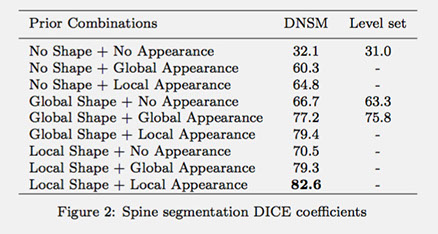
The proposed algorithm is implemented in C++ using Insight Segmentation and Registration Toolkit (ITK) [1]. Next, we give the results of two experiments. In the first experiment, we show the application of the DNSM shape and appearance priors when training samples are available. Figure 1 shows the segmentation example of a dendritic spine. We segmented 40 spines in a leave-one-out manner using 2-photon microscopy images, and Figure 2 summarizes the average DICE score obtained using the different shape and appearance prior combinations. It can be seen from Figure 2 that the result improves as we go from no priors to global priors, and then to local priors (for both shape and appearance). The table in Figure 2 also compares segmentation using DNSM priors with level set based priors of [2].

 

In the second experiment, we show the results of using the DNSM as a parametric level set framework for two-phase and multiphase image segmentations. We compare our result with conventional region-based level set method of Chan and Vese (CV) using both their two-phase [3] and multiphase (CV multiphase) [4] methods. Figure 3 shows segmentation results of three different two-phase images using DNSM (on the second row) and CV (on the third row) methods. The DNSM based parametric level set achieves equivalent or better segmentation results with a computational speed of around 10 times compared to the sparse implementation of the CV method.

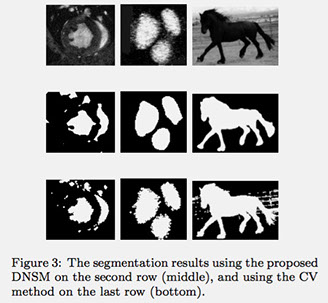
Figure 4 compares the segmentation performances of the DNSM-multiphase (second row) with the standard CV-multiphase level set (third row), when random initialization is used. The proposed DNSM-multiphase method is less sensitive to initialization and it requires a (almost) constant computational time independent of the number of objects to be simultaneously segmented.

 

References:

 

[1] L. Ibanez, W. Schroeder, L. Ng, and J. Cates. The ITK Software Guide: The Insight Segmen- tation and Registration Toolkit (version1.4). Kitware, 2003.

 

[2] J. Kim, M. Cetin, and A.S. Willsky. Nonparametric shape priors for active contour-based image segmentation. Signal Processing, 87(12):3021 – 3044, 2007.

 

[3] T.F. Chan and L.A. Vese. Active contours without edges. Image Processing, IEEE Transactions on, 10(2):266–277, Feb 2001.

 

[4] L.A. Vese and T.F. Chan. A multiphase level set framework for image segmentation using the mumford and shah model. International Journal of Computer Vision, 50(3):271–293, 2002.