
Scientific Computing and Imaging Institute
University of Utah
phone: (801)587-9933
CV
Research interests
My research interests in in computer graphics, in particular in point-based graphics, surface modeling and representation and surface reconstruction from noisy data.
Selected publications
|
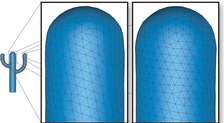
Accepted to SGP 2005 We introduce an algorithm for constructing a high-quality triangulation directly from Point Set Surfaces. Our algorithm requires no intermediate representation and no post-processing of the output, and naturally handles noisy input data, typically in the form of a set of registered range scans. It creates a triangulation where triangle size respects the geometry of the surface rather than the sampling density of the range scans. Our technique does not require normal information, but still produces a consistent orientation of the triangles, assuming the sampled surface is an orientable two-manifold. Our work is based on using Moving Least-Squares (MLS) surfaces as the underlying representation. Our technique is a novel advancing front algorithm, that bounds the Hausdorff distance to within a user-specified limit. Specifically, we introduce a way of augmenting advancing front algorithms with global information, so that triangle size adapts gracefully even when there are large changes in surface curvature. Our results show that our technique generates high-quality triangulations where other techniques fail to reconstruct the correct surface due to irregular sampling on the point cloud, noise, registration artifacts, and underlying geometric features, such as regions with high curvature gradients. |

|
Accepted to SIGGRAPH 2005 We introduce a robust moving least-squares technique for reconstructing a piecewise smooth surface from a potentially noisy point cloud. We use techniques from robust statistics to guide the creation of the neighborhoods used by the moving least squares (MLS) computation. This leads to a conceptually simple approach that provides a unified framework for not only dealing with noise, but also for enabling the modeling of surfaces with sharp features. Our technique is based on a new robust statistics method for outlier detection: the forward-search paradigm. Using this powerful technique, we locally classify regions of a point-set to multiple outlier-free smooth regions. This classification allows us to project points on a locally smooth region rather than a surface that is smooth everywhere, thus defining a piecewise smooth surface and increasing the numerical stability of the projection operator. Furthermore, by treating the points across the discontinuities as outliers, we are able to define sharp features. One of the nice features of our approach is that it automatically disregards outliers during the surface-fitting phase. |

|
SIGGRAPH 2003 - ACM TOG 22(3) We present an anisotropic mesh denoising algorithm that is effective, simple and fast. This is accomplished by filtering vertices of the mesh in the normal direction using local neighborhoods. Motivated by the impressive results of bilateral filtering for image denoising, we adopt it to denoise 3D meshes; addressing the specific issues required in the transition from two-dimensions to manifolds in three dimensions. We show that the proposed method successfully removes noise from meshes while preserving features. Furthermore, the presented algorithm excels in its simplicity both in concept and implementation. |
|
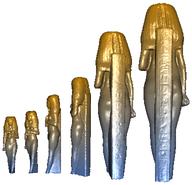
ACM TOG 22 (4) Progressive point set surfaces (PPSS) are a multilevel point-based surface representation. They combine the usability of multilevel scalar displacement maps (e.g. compression, filtering, geometric modeling) with the generality of point-based surface representations (i.e. no fixed homology group or continuity class). The multiscale nature of PPSS fosters the idea of point-based modeling. The basic building block for the construction of PPSS is a projection operator, which maps points in the proximity of the shape onto local polynomial surface approximations. The projection operator allows the computing of displacements from smoother to more detailed levels. Based on the properties of the projection operator we derive an algorithm to construct a base point set. Starting from this base point set, a refinement rule using the projection operator constructs a PPSS from any given manifold surface. |
| |
Presented IEEE Visualization 2001, journal version in IEEE TVCG 2003 9 (1) We advocate the use of point sets to represent shapes. We provide a definition of a smooth manifold surface from a set of points close to the original surface. The definition is based on local maps from differential geometry, which are approximated by the method of moving least squares (MLS). We present tools to increase or decrease the density of the points, thus, allowing an adjustment of the spacing among the points to control the fidelity of the representation. To display the point set surface, we introduce a novel point rendering technique. The idea is to evaluate the local maps according to the image resolution. This results in high quality shading effects and smooth silhouettes at interactive frame rates. |