1D Manufactured Solutions for a
Vibrating Wire
Philip Wallstedt – September 2007
The method of manufactured
solutions (Banerjee 2006, Schwer 2002, Knupp and Salari 2003) allows numerical
computer codes to be verified even when they involve nonlinear relations for
which exact solutions will never be found. A solution of appropriate
difficulty is assumed and a source term is added to the equations that makes
the solution true. The pitfalls of “eye ball norms” and rough comparisons
with linear solutions are avoided allowing for thorough and precise
demonstration of numerical convergence.
A 1D elastic wire vibrates
length-wise. For case 1 the wire is fixed at both ends; for case 2 the
wire is fixed at one end with zero stress at the free end. The amplitude
of the vibrations is large enough that dynamic behavior is non-linear.
Notation
X = reference position
x = current position
u = x – X = displacement
![]() = deformation
gradient
= deformation
gradient
J = F = Jacobian (Poisson’s ratio
is zero)
P = 1st Piola-Kirchhoff
stress
![]() = Cauchy stress
= Cauchy stress
![]() = density
= density
a = acceleration
b = acceleration due to body force
Y = Young’s Modulus
![]() = wave speed
relation
= wave speed
relation
A = maximum wire displacement
Governing and Constitutive Equations
Numerical solid mechanics methods
use the Updated Lagrangian formulation. However it is more convenient to
manufacture solutions in the Total Lagrangian form. Either form is
correct and they produce equivalent solutions (Belytschko 2000).
|
|
Total Lagrangian [Belytschko p194] |
Updated Lagrangian [Belytschko p143] |
|
|
Governing Equation |
|
|
(1) |
|
Neo-Hookean Constitutive Equation |
[Belytschko p239, p103] |
|
(2) |
|
1D, Poisson’s Ratio = zero, |
|
|
(3) |
For both manufactured solutions
the body force is used as the source term.
Case 1
The displacement for all places
and times within the wire is assumed to be:
![]()
(4)
This solution is substituted into
the terms of the governing equation:
![]()
(5)
![]()
(6)
![]()
(7)
![]()
(8)
The governing equation (1)
becomes:
![]()
(9)
Noting that ![]() the following body force acceleration must be applied
to make the solution valid:
the following body force acceleration must be applied
to make the solution valid:
![]()
(10)
where u and F are defined via (4)
and (5).
The PDE is briefly restated: Given
![]() on [0,1] where
on [0,1] where ![]() , the displacement within the wire at any time is
, the displacement within the wire at any time is ![]() .
.
A solid mechanics model is used to
solve the problem with 10% deformation.
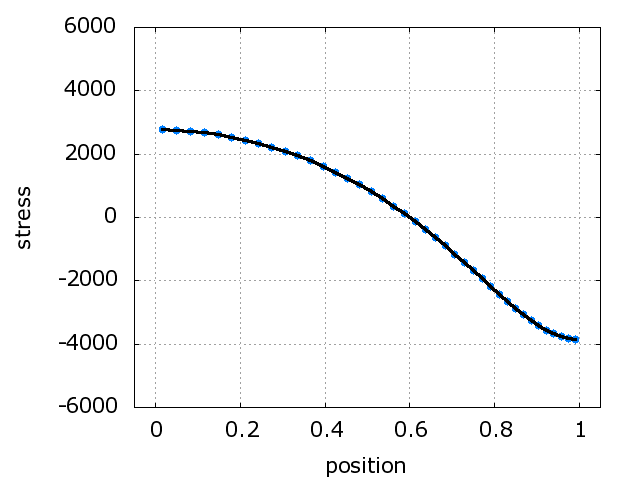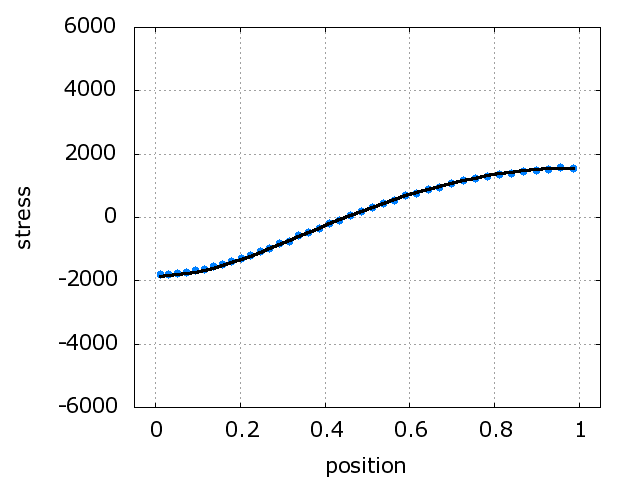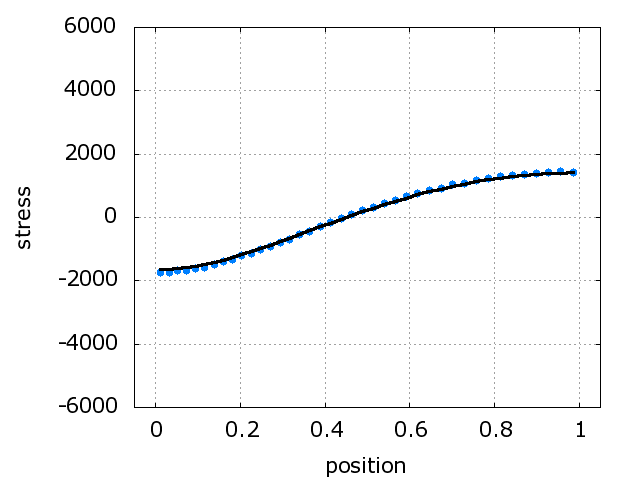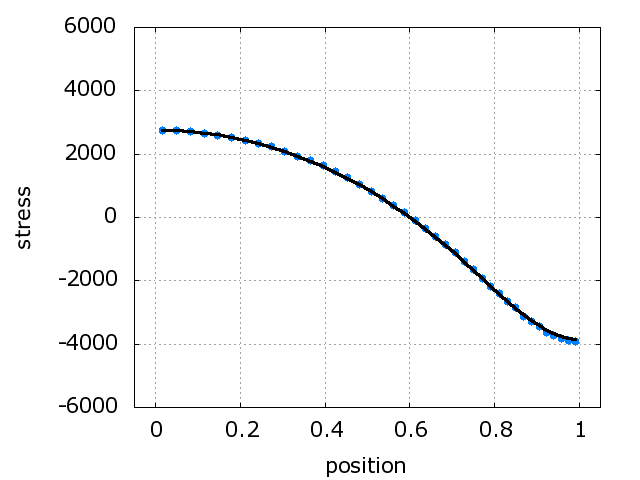
Case 2
The displacement for all places
and times within the wire (of initial length L) is assumed to be:
![]()
(11)
This solution is substituted into
the terms of the governing equation:
![]()
(12)
![]()
(13)
![]()
(14)
The governing equation (1)
becomes:
![]()
(15)
Noting that ![]() the following body force acceleration must be applied
to make the solution valid:
the following body force acceleration must be applied
to make the solution valid:
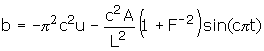
(16)
where u and F are defined via (11)
and (12).
The PDE is briefly restated: Given
![]() on [0,L] where the body force (acceleration) is defined
by (16), the displacement within the wire at any time is
on [0,L] where the body force (acceleration) is defined
by (16), the displacement within the wire at any time is ![]() .
.
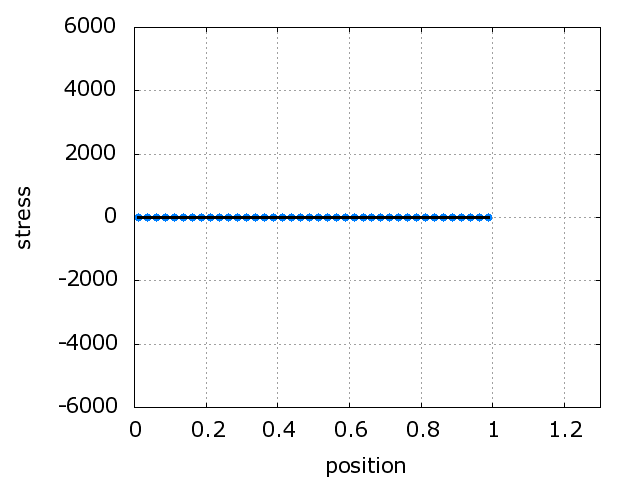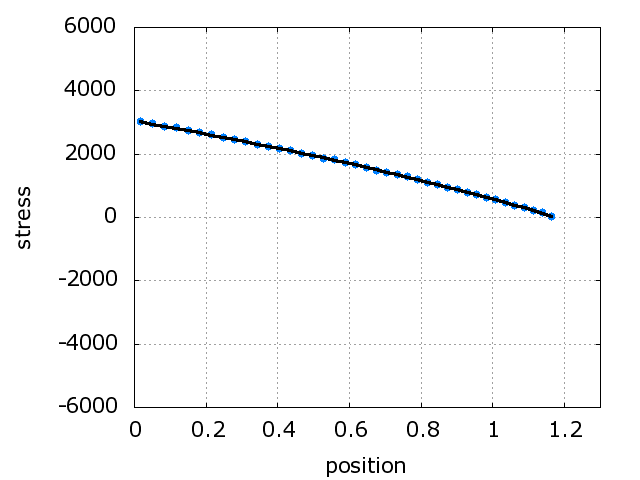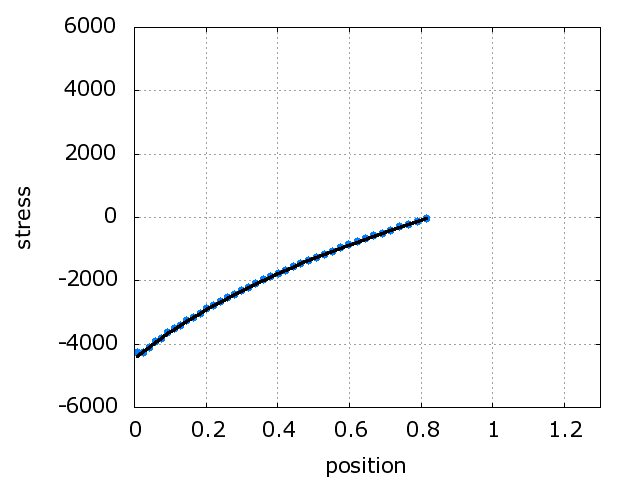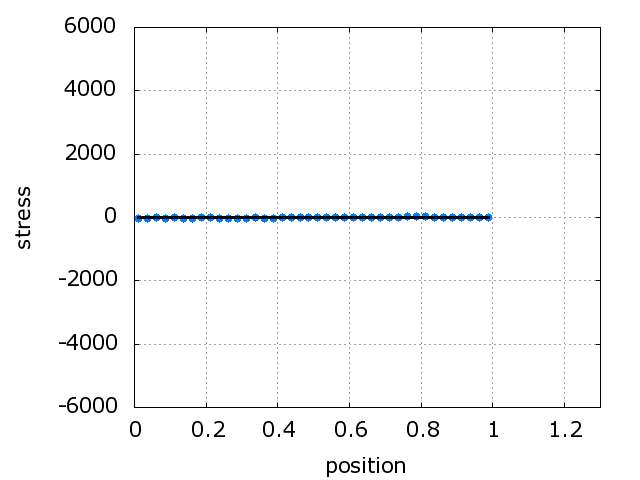
The problem is solved with 20%
deformation.
References
Banerjee, Biswajit (2006) “Method
of Manufactured Solutions”; available online at http://www.eng.utah.edu/~banerjee/Notes/MMS.pdf
Belytschko T., Liu W. K., Moran B.
(2000) “Nonlinear Finite Elements for Continua and Structures”; John Wiley and
Sons Ltd.
Knupp P., Salari K. (2003)
“Verification of Computer Codes in Computational Science and Engineering”;
Chapman & Hall/CRC.
Schwer, Len (2002) “Method of
Manufactured Solutions: Demonstrations”; available online at http://www.usacm.org/vnvcsm/PDF_Documents/MMS-Demo-03Sep02.pdf