Overview

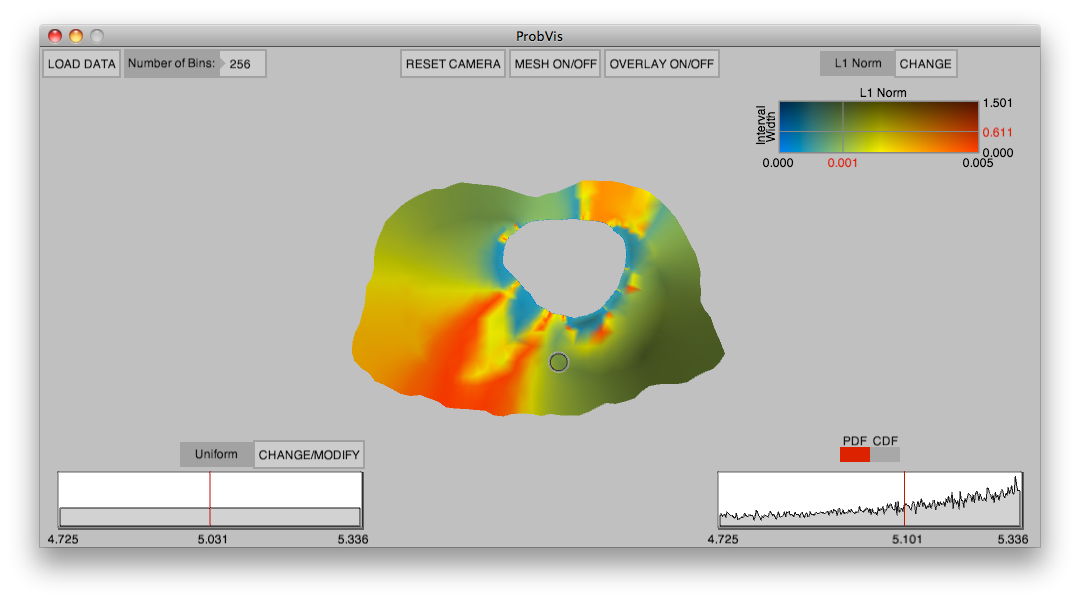
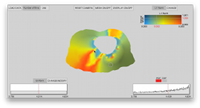
The ProbVis software tool allows for the interactive display and exploration of a spatial collection of data distributions. A global display shows the value of a difference measure across the spatial domain. The user can change the measure from the L1 Norm to the Hellinger distance. The user is also given a pointer to explore the individual distributions which are diplayed as a PDF or CDF in the lower corner.

Software

ProbVis is written using the Processing programming language. To run the standalone applications simply download the tarball for your platform, uncompress, and double-click on the ProbVis icon. The source code is a Processing sketch which can be run and modified using the Processing framework, freely available at Processing.org.

Data

The software tool allows the user to investigate any dataset, as long as conforms to our format. The data should be in its own directory, and separated into 3 files: geometry.txt, connectivity.txt, and data.txt. The names of these files must match exactly, and none have headers.

• geometry.txt This file describes the 3D points of the spatial domain. Each point should be written on a single line, (x, y, z), seperated by a space.
• connectivity.txt This file describes the triangles of the spatial domain. Each triangle is written on a single line, and the three points are defined by indices from geometry.txt.
• data.txt This file holds the data distribution at each point. Each line will contain all data samples for a single point. The order of the points should be the same as geometry.txt. Any number of samples is allowed, as long as it is the same number for every point.

Four examplary data sets are provided:

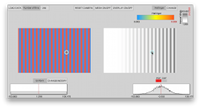
• Alternating This dataset defines an alternating pattern across the rectangular spatial domain. Gaussian and uniform distributions are alternated along the x-axis, as is the interval width.
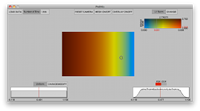
• Shape This dataset linearly blends from a normal to a uniform distribution along the x-axis.
• Interval This dataset is uniform across the entire spatial domain, but increases the interval width along the x-axis.
• Torso This dataset is the result of solving the bioelectric forward problem across a 2D torso domain using poynomial chaos.

Publication

Interactive Visualization of Probability and Cumulative Density Functions
Kristin Potter, Robert M. Kirby, Dongbin Xiu, & Chris R. Johnson
International Journal for Uncertainty Quantification, to appear. 2011.

Movies

Alternating	Interval	Shape	Torso

Contact

Kristi Potter kpotter@sci.utah.edu SCI Institute University of Utah

Robert M. Kirby kirby@sci.utah.edu SCI Institute University of Utah

Dongbin Xiu dxiu@purdue.edu Dept of Mathematics Purdue University

Chris R. Johnson crj@sci.utah.edu SCI Institute University of Utah

Acknowledgements

This is a collaborative research project supported under NSF IIS-0914564, NSF IIS-0914447 and through DOE NETL DE-EE0004449, and NIH 2P41 RR0112553-12 (Johnson). Infrastructure support provided through NSF-IIS-0751152.