Design of 2D Time-Varying Vector Fields

IEEE Transactions on Visualization and Computer Graphics, 2011

Guoning Chen1, ViVek Kwatra2, Li-Yi Wei3, Charles Hansen1 and Eugene Zhang4

1 SCI Institute, University of Utah

2 Google Inc

3 University of Hong Kong

4 Oregon State University

 

 

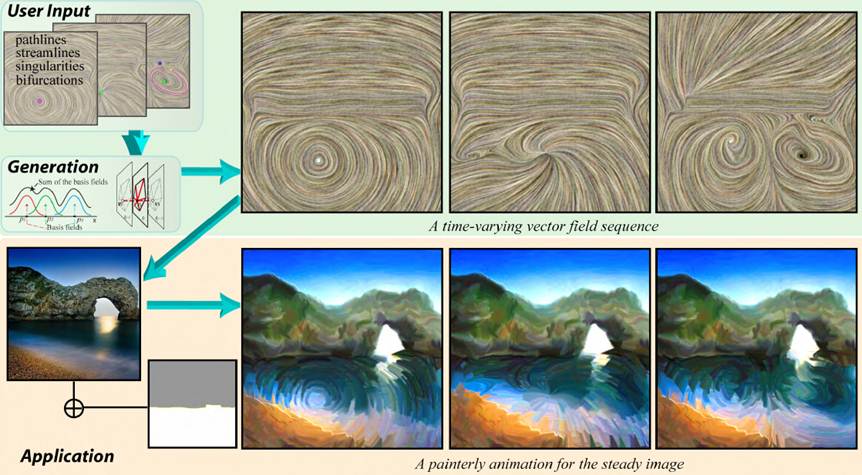
This figure shows the pipeline of the presented design system for 2D time-varying vector fields. First, the user specifies the desired flow behaviors in the forms of spatial-temporal constraints. The system then produces a time-varying vector field that matches the constraints. The obtained field is then applied to computer graphics applications to create various dynamic effects. Here, we apply the obtained fields to produce painterly animation from a single image. Note that we use the created time-varying vector field to orient and move the brush strokes in the lower part of the image to achieve an artistic water wave effect: the vortex rotates, moves and changes its characteristics, then splits into two vortices at the end. Please see the accompanying video for this animation. The inset plot shows the changes of the consecutive instantaneous fields in terms of the total variance of the vector values in the space.

 

 

Abstract

    Design of time-varying vector fields, i.e., vector fields that can change over time, has a wide variety of important applications in computer graphics. Existing vector field design techniques do not address time-varying vector fields. In this paper, we present a framework for the design of time-varying vector fields, both for planar domains as well as manifold surfaces. Our system supports the creation and modification of various time-varying vector fields with desired spatial and temporal characteristics through several design metaphors, including streamlines, pathlines, singularity paths, and bifurcations. These design metaphors are integrated into an element-based design to generate the time-varying vector fields via a sequence of basis field summations or spatial constrained optimizations at the sampled times. The key frame design and field deformation are also introduced to support other user design scenarios. Accordingly, a spatial-temporal constrained optimization and the time-varying transformation are employed to generate the desired fields for these two design scenarios, respectively. We apply the time-varying vector fields generated using our design system to

a number of important computer graphics applications that require controllable dynamic effects, such as evolving surface appearance, dynamic scene design, steerable crowd movement, and painterly animation. Many of these are difficult or impossible to achieve via prior simulation-based methods. In these applications, the time-varying vector fields have been applied as either orientation fields or advection fields to control the instantaneous appearance or evolving trajectories of the dynamic effects.

Paper

 

Acrobat [pdf (~8.5MB)]

Bibtex

entry

@ARTICLE{Chen:TimeVarying:2011,
    author    =  {Guoning Chen and Vivek Kwatra and Li-Yi Wei and Charles Hansen and Eugene Zhang},
    title         =  {Design of 2D Time-Varying Vector Fields},
    journal    =  {IEEE Trans. Visualization and Computer Graphics},
    year        =  {2011},
    volume   =  {},
    number  =  {},

note = {to appear},

page = {},
}

Video

  QT movie (8 mins, ~66MB)

Results

    bunny2    hept2     letters2

     Time-varying surface appearance

 

   storms2     leaves2     writing_grass2

     Time-varying natural and artistic-like effects

 

   crowds1

      Steerable crowds

 

   painting    burnning_sun2

      Non-photo-realistic rendering

Source code

The source code (and a short manual) of this project is available [here]. It was written using C++ and compiled under Visual Studio 2005 and later. NOTE that the source code is for the use of the research purpose only.

Acknowledgment
  • People

        Dr. Mark van Langeveld

 

  • Funding

   NSF (CCF-054881 award and IIS-0546881)

        DOE SicDAC VACET

        KAUST Award No. KUS-C1-016-04

 

Research Projects Related to NSF Grant CCF-0546881

This material is based upon work supported by the National Science Foundation under Grant No. 0546881.

Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation (NSF).