Workshop on TDA in Biomedicine (ACM-BCB 2016)

International Workshop on Topological Data Analysis in Biomedicine (TDA-Bio)
Seattle, WA, October 2, 2016

Part of the 7th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics (ACM-BCB)

Overview

Biomedical Informatics in the Big Data Era

Data sets of different forms in biomedical sciences have seen a huge increase in size and complexity in the past two decades. We have made substantial progress in various aspects of genomics, e.g., mapping of whole genomes of humans as well as other small and large species. Similarly, a lot has been explored in the scope of the sequence-to-structure-to-function paradigm for proteins. At the same time, current data challenges in biomedicine are much more diverse, as well as varied in scope. The sheer scale and diversity of data sources and types encountered in today's biomedical data sets often render the routine computational techniques ineffective.

Recently, a suite of new techniques termed topological data analysis (TDA) has shown a lot of promise in discovering structure in large, high-dimensional, and diverse data sets that other traditional techniques could not find. The range of applications includes gene expression analysis, voting, and basketball players' performances, to name a few. This workshop will present a concise yet self-contained overview of the key aspects of TDA, with an eye toward motivating the application of these techniques to problems in bioinformatics and computational biology (BCB). While topological techniques have been applied previously in certain subfields of BCB (e.g., to model protein and DNA/RNA 3D structure), they have proved to be much more versatile and powerful than these applications might suggest. We aim to showcase the versatility and strength of this suite of techniques in this workshop.

Why Topology?

Topology is the branch of mathematics that studies the shapes of spaces, and how spaces are connected. Until recently, topology has concentrated mostly on abstractly defined shapes and surfaces. However, in the past two decades, there has been a concerted effort to adapt topological methods to various applications, one of which is the study of large and high-dimensional data sets.

There are many important properties of topology that make efficient extraction of patterns from large data sets possible. First, topology studies shapes in a coordinate free way. In other words, topological constructions will not depend on the coordinate system chosen, but only on the distances between points in the data set. This will enable comparison among data sets derived from different platforms or coordinate systems. Second, topological constructions are not sensitive to small changes in data, and are robust against noise. Third, topology works with compressed representations of spaces in the form of simplicial complexes (e.g., triangulations), which can be viewed as a form of compression that preserves information relevant to how points are connected. Topological methods are also known to be more sensitive to both large and small scale patterns than other more traditional techniques such as principal component analysis (PCA), multidimensional scaling (MDS), and cluster analysis. Further, the "shapes" of the topological representations (simplicial complexes in general) naturally lend themselves to insightful visualization.

The Workshop

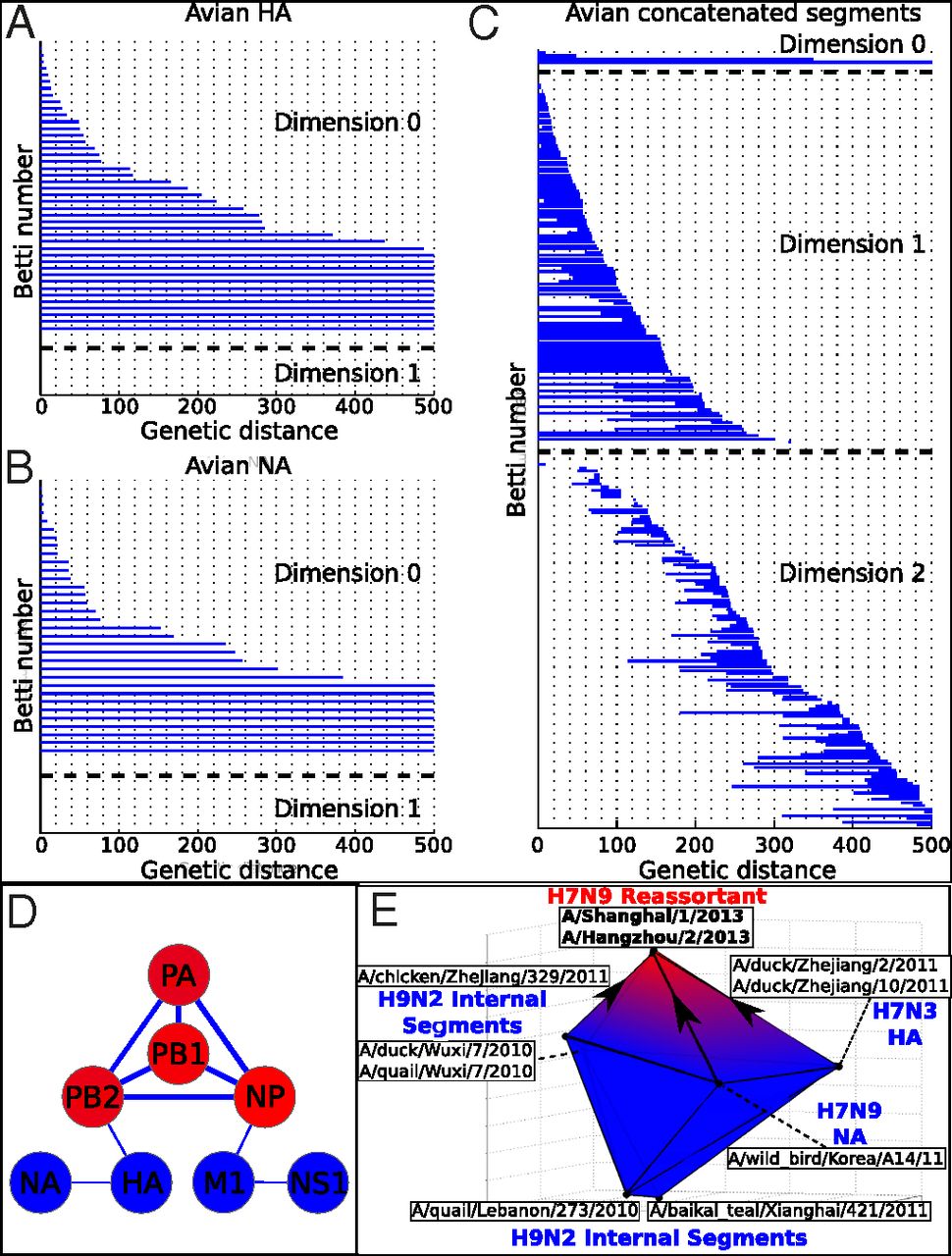This workshop will expose the audience to the key fundamental as well as computational aspects of topology. The speakers will introduce (within their talks) basic TDA concepts and techniques, such as simplicial complexes, homology, persistent homology, Reeb graphs and mapper. They will also present how these concepts and techniques have been, or potentially could be, employed to tackle interesting problems in several areas of BCB.

(source: PNAS)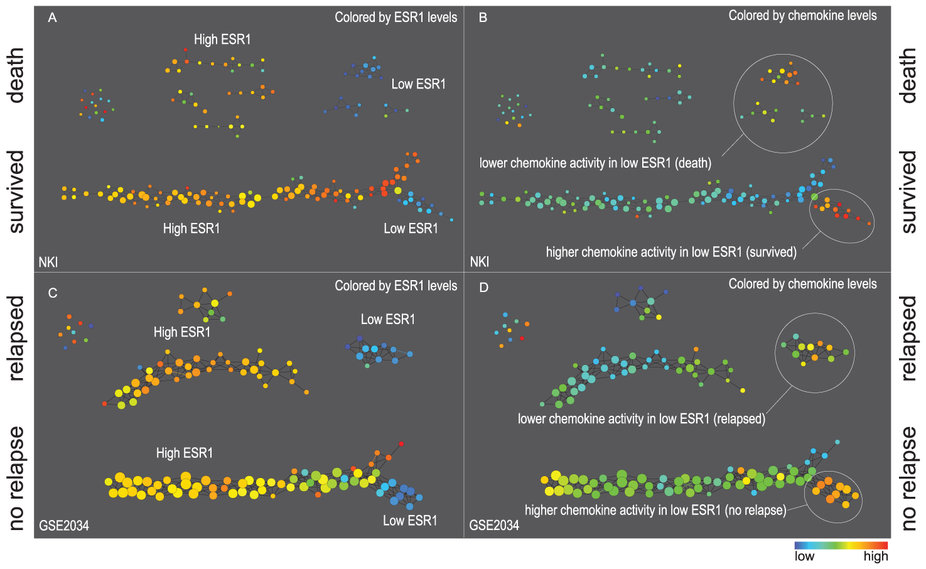

(source: Nature Scientific Reports)

Tentative Schedule

Since TDA is a relatively new area to the ACM-BCB audience, our plan will be to maximize the involvement of the audience in the workshop. To this end, we plan a full day format, with two sessions. With an eye toward increasing the exposure to students and junior researchers, we plan to have a demo session. We will also have a panel discussion on the potential applications of TDA in the BCB domain.

All talks would be designed to be accessible to a general BCB audience. The speakers would also encourage increased participation from the audience, by budgeting enough time for questions during as well as at the end of their talks.

Potential topics to be covered in the workshop would include: (a) general introduction to TDA, concepts, techniques, and software; (b) analysis of high-dimensional biomedical data; (c) TDA on biological and brain networks; (d) image segmentation; (e) TDA on phylogenetic trees; and much more. Keynote talks will be 40 minutes long with 10 minutes for questions. Invited talks will be 30 minutes long with 5 minutes for questions.

Time	Description	Speaker	Title
8:50 - 9:00	Opening remarks
9:00 - 9:50	Keynote Talk 1	Yusu Wang Associate professor of computer science at the Ohio State University	Two Examples of Application of Topological Methods in Neuron Data Analysis
10:00 - 10:35	Invited Talk 1	Chao Chen Assistant professor of computer science at City University of New York	Extracting and Using Topological Structures in the Analysis of Biomedical Images
10:35 - 10:50	Break
10:50 - 11:25	Invited Talk 2	Elizabeth Munch Assistant professor of mathematics at University at Albany	Utilizing Topological Data Analysis to Detect Periodicity
11:30 - 12:05	Invited Talk 3	Brittany Fasy Assistant professor of computer science at Montana State University	Using Topological Data Analysis to Study Glandular Architecture
12:05 - 13:30	Lunch
13:30 - 14:20	Keynote Talk 2	Gunnar Carlsson Professor of mathematics at Stanford University President and co-founder of Ayasdi	The Shape of Biomedical Data
14:30 - 15:20	Software Demo	Svetlana Lockwood PostDoc Fellow, Washington State University	Open Source Software for TDA
15:20 - 15:25	Break
15:25 - 16:00	Invited Talk 4	Bei Wang Phillips Assistant professor of computer science at the University of Utah	Topological Data Analysis for Brain Networks
16:00 - 16:35	Invited Talk 5	Michael Robinson Assistant Professor of Applied Mathematics at the American University	Finding Cross-Species Orthologs with Local Topology
16:40 - 17:10	Panel Discussion
17:10 - 17:15	Closing remarks

Talk Abstract

Keynote Talk 1

Yusu Wang

Title: Two Examples of Application of Topological Methods in Neuron Data Analysis

Abstract: In this talk, I will describe two of our recent efforts in analyzing neuron structures via topological methods. The first topic is neuron shape comparison via persistent homology. Persistent homology is an important development in the field of applied and computational topology in the past 15 years. It provides a way to summarize an input domain the lens of a specific filtration of the domain. We show how the persistence summary can be used to compare neuron trees. The second topic is neuron reconstruction via Morse theory. We presend a framework to automatically extract neuron tree structures from 2D / 3D images with the help of discrete Morse theory. We will give some preliminary results in each of these two directions. This is joint work with Yanjie Li, Suyi Wang, Partha Mitra and Giorgio Ascoli.

[Slides] [Talk Video]

Keynote Talk 2

Gunnar Carlsson

Title: The Shape of Biomedical Data

Abstract: The life sciences produce data sets which are often complex, and are not easily addressed by standard algebraic methods of modeling. This situation calls for new methods of modeling, and one such is topological modeling, based on the mathematical subdiscipline of topology. Roughly speaking, topology studies shape and its higher dimensional analogues, and can be adapted to the setting of point clouds, where most data sets reside. In this talk, we will discuss this methodology with numerous examples.

[Slides] [Talk Video]

Invited Talk 1

Chao Chen

Title: Extracting and Using Topological Structures in the Analysis of Biomedical Images

Abstract: In this talk, we will demonstrate how topological structures can be extracted and used in the analysis of cardiac and neuron images. In these cases, existing segmentation methods are challenged by lack of shape priors and inhomogeneity of the appearance. We show how topological information can form novel global prior and be used in the segmentation model. In the second half, we show how topological structures can help the clustering of high-dimensional discrete data, e.g., DNA data.

[Slides] [Talk Video]

Invited Talk 2

Elizabeth Munch

Title: Utilizing Topological Data Analysis to Detect Periodicity

Abstract: The field of TDA has shown itself to be a very powerful tool for data anlysis, finding structure not easily detectible by other methods. In this talk, we will look at two applications of TDA to time series where it is necessary to quantify periodicity in the system. The ability for TDA to accept different types of input means that these data come as time series in a broad sense, mean that the output could be real numbers, images, higher dimensional values, etc. The first application comes from engineering, where chatter behavior in a turning process leads to the finished parts being unuseable. In this application, we use Takens embedding on the real-valued time series to obtain a point cloud which can be investigated using persistent homology. The second application comes from atmospheric science, where persistent homology applied to a time series of IR images of a hurricane gives quantification of a periodic behavior previously only qualitatively described by domain scientists. These applications show that the techniques presented can be used on domain from a wide range of domains, as well as having the potential to find more complex behavior than just periodicity.

[Slides] [Talk Video]

Invited Talk 3

Brittany Fasy

Title: Using Topological Data Analysis to Study Glandular Architecture

Abstract: The current standard for prostate cancer grading is the Gleason score, a subjective rating system based on an analysis of high-level tissue architecture and glandular shape and organization. This analysis can be aided with tools from topological data analysis. In particular, we use persistence diagrams, intensity plots (or persistence images), landscapes, and silhouettes as descriptors of the biopsy slides. We will discuss preliminary results on comparing regions of pure Gleason grades 3, 4, and 5.

Other biological applications of TDA we will briefly discuss are finding correlations between biofilms and quantifying the significance of bubbles in De Bruijn graphs.

[Slides]

Invited Talk 4

Bei Wang Phillips

Title: Topological Data Analysis for Brain Networks

Abstract: In this talk, we present a novel method for analyzing the relationship between functional brain networks and behavioral phenotypes. Drawing from topological data analysis, we first extract topological features using persistent homology from functional brain networks that are derived from correlations in resting-state fMRI. Rather than fixing a discrete network topology by thresholding the connectivity matrix, these topological features capture the network organization across all continuous threshold values. We then propose to use a kernel partial least squares (kPLS) regression to statistically quantify the relationship between these topological features and behavior measures. The kPLS also provides an elegant way to combine multiple image features by using linear combinations of multiple kernels. In our experiments we test the ability of our proposed brain network analysis to predict autism severity from rs-fMRI. We show that combining correlations with topological features gives better prediction of autism severity than using correlations alone.

[Slides] [Talk Video]

Invited Talk 5

Michael Robinson

Title: Finding Cross-Species Orthologs with Local Topology

Abstract: Functionally and genetically related proteins from different species are called "orthologs". Knowledge about well-studied proteins in one species can be transferred to their othologs in other species. Since proteins are best understood both in genetic and functional contexts -- both realized as networks -- the problem of finding pairs of orthologs is related to network alignment problems. Various methods for network alignment exist, but they are difficult to employ at scale and tend to prefer global structure at the expense of local structure in the network.

This talk will present a novel multi-stage topological prefilter that reduces the search space for pairs of orthologs dramatically. We will focus our attention on networks of protein-protein interactions (PPI), which can be useful in predicting protein function or identifying possible causes of disease. Proteins within and across species can also be classified in common orthologous groups (COGs) based upon their inferred ancestry. Using these two networks and our prefilter, we discovered local homological and local spectral features of the flag complex on hybrid protein-protein and protein-gene networks that appears to detect certain classes of cross-species orthologs.

[Slides] [Talk Video]

Software Demo

Svetlana Lockwood

Title: Open Source Software for TDA

Abstract: Topological data analysis (TDA) is a new and vibrant research field. The application of TDA ranges over a variety of disciplines from biological and brain networks to image segmentation to phylogenetic trees. In this demo we present open source software for two most popular methods of topological data analysis. The first method is based on persistent homology and is used to study the shape and the connectivity of the data space. The second method follows from the Reeb graph construction and is commonly known as Mapper. We present case studies for both methods complete with examples and code.

[Slides] [Talk Video] (Apologies for some technical issues associated the presentation.) [Demo Code]

Panel Discussions

[Video]

Registration

Please register through ACM-BCB.

Early registration deadline: August 15.

There is no separate registration for the workshop.

Graduate Student Travel Support

We expect some funding from NSF (CCF-1654106) to support the participation of graduate students in the workshop. We will be able to support the registration and travel of up to $1000 per person for eight student participates.

If you're an interested student, please apply (advisors, please encourage your students to apply).

Graduate students will be required to submit an online application to the organizers outlining their background, research interests, and reasons for why they want to attend TDA-Bio. Each applicant would also be required to arrange for one letter of recommendation and support from their advisor to be sent to the organizers. The advisor (or the student's Department or Program Chair) should also commit to cover the cost of the student's travel to TDA-Bio in excess of the award. Students from underrepresented groups are especially encouraged to apply.

Please apply via the Google application form.

The deadline for travel support application is August 12th.

Decisions will be made by August 13 before the early registration deadline on August 15.

Students are also encouraged to apply for general travel grant from ACM-BCB.

Organizers

Bala Krishnamoorthy
Associate Professor
Department of Mathematics and Statistics
Washington State University
bkrishna AT math.wsu.edu

Bei Wang Phillips
Assistant Professor
School of Computing
Scientific Computing and Imaging Institute
University of Utah
beiwang AT sci.utah.edu

Acknowledgment

The graduate student travel grant is provided by the National Science Foundation CCF-1654106 . Any opinions, findings, and conclusions or recommendations expressed in this workshop are those of author(s)/speaker(s) and do not necessarily reflect the views of the National Science Foundation.

Web page last update: October 15, 2016.