Objective 1- Validation of Hip
Joint FE models
·
Reconstruction
of Pelvic Geometry from Volumetric CT Images.
·
Determination
of Cortical Thickness for the Pelvis.
·
Errors in
Estimation of Cortical Thickness using CT.
·
Geometric
Accuracy of Subject-specific FE Model of the Pelvis.
·
Subject-specific
Modeling of the Mechanics of the Pelvis.
· Experimental Measurement and Finite Element Prediction of Cartilage Contact Stresses in the Hip.
Objective 2 – Patient-Specific FE
Modeling of Acetabular Dysplasia (ongoing work)
·
Generation
of Patient-specific Models of the Hip and Pelvis from
Introduction
Improved methods for quantifying the stress
distribution in and around the hip may improve implant designs, surgical
approaches, diagnosis and treatment of disorders such as dysplasia, and provide
the framework necessary for preoperative surgical planning. It is difficult to assess the stress and strain
distribution throughout the entire hip joint using simplified
mathematical models, implanted prostheses, or via experiments with cadaveric
tissue. An alternative approach to
analyze hip joint mechanics is the finite element (FE) method, which can accommodate
large inter-subject variations in tissue geometry and material properties. The potential benefit of patient-specific FE
analysis becomes clear when one considers how difficult (if not impossible) it
would be to assemble a population of donor tissue that exhibits a specific
pathology such as pelvic dysplasia.
Although finite element (FE) models of the hip joint have been
developed, validation by direct comparison with subject-specific experimental
measurements of both bone strains and cartilage contact stress has not been
performed. Previous FE models of the hip
joint have often used gross simplifications regarding tissue geometry and
material properties. While it may be acceptable to model the hip joint with
idealized geometry and material properties for some applications, it is absolutely
crucial to use accurate inputs if the research objective is to study patient-specific
biomechanics. The overall objectives of
this research study are to 1) develop and validate methods to generate
patient-specific FE models of the human hip joint, and 2) analyze
patient-specific FE models of acetabular dysplasia.
Objective
1- Validation of Hip Joint FE models
Reconstruction of Pelvic Geometry from Volumetric CT
Images. To evaluate our ability to reconstruct pelvic geometry
from volumetric CT images, a volumetric CT scan of a cadaveric pelvis of a 68
y/o female was obtained. The sacroiliac
joint and all soft tissues, with the exception of articular cartilage, were
removed. A CT scan (512x512 acquisition
matrix, FOV=225 mm, in-plane resolution=0.44x0.44 mm, slice thickness=0.6 mm,
354 slices) was obtained in a superior to inferior fashion using a
Marconi-MX8000 scanner (Philips
Medical Systems,
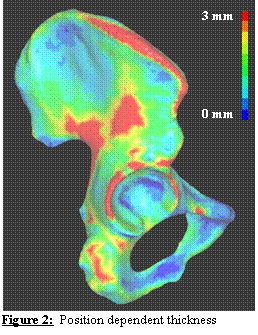Determination of Cortical Thickness for the Pelvis. The
deformation of the pelvis and femur can dramatically change the measured
contact stresses in the hip [1]. Most of the
load on the pelvis is borne by the cortical bone, so it is crucial to model the
thickness of the pelvic cortex accurately. To this end, a novel algorithm was
developed to automatically assign a spatially varying cortical shell thickness
to the cortical shell elements based on the distances between the two polygonal
surfaces. The algorithm was tested using
concentric spheres, boxes, and parallel planes with known thickness and varying
mesh densities. Weight factors were
implemented to account for areas of high curvature (such as those at the edges
of a box or around the acetabular rim).
The RMS thickness error for all test meshes was determined to be +/-
2%. Patient-specific cortical bone
thickness for a cadaver pelvis FE model is presented in Figure 2.
Errors in Estimation of Cortical Thickness using CT. It
is well known that CT overestimates the thickness of cortical bone [2]. However, the
amount of error depends on the CT scanner and settings. The errors in estimation of thickness from CT
were assessed in a preliminary study. A
custom-built phantom was used to assess the accuracy of cortical thickness
measurements (Figure 3, left panel) [37].
Ten aluminum tubes (wall thickness 0.127– 2.921 mm) were fit into a 70
mm dia. Lucite disc. The centers of the
aluminum tubes were filled with Lucite rods so that both the inner and outer
surfaces of the tubes were surrounded by a soft tissue equivalent material
[38,39]. Aluminum has x-ray attenuation
coefficient that is similar to cortical bone [37]. The phantom was scanned with the same CT
scanner field of view and energy settings above. The z-axis of the scanner was aligned flush
with the top edge of the tissue phantom to prevent volume averaging between
successive slices. The inner and outer circumferences of the tubes were segmented
from the CT image data using the technique described above. The thickness algorithm was used to determine
wall thickness.
Thickness was measured accurately
down to 0.7 mm thick with less than 10% error, which was consistent with the
work of the others [3]. We are
currently enhancing this algorithm to improve its accuracy even further by
taking into account the CT signal attenuation that occurs for very thin
structures (Figure 3, right panel).
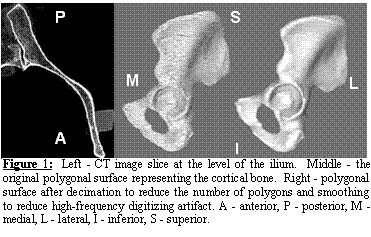
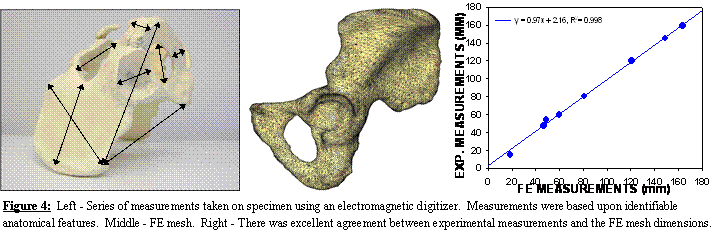
Geometric
Accuracy of Subject-specific FE Model of the Pelvis. Using the polygonal surface of Figure 1 we
constructed a FE model consisting of 30,000 triangular shell elements for
cortical bone and 210,000 tetrahedral solid elements for trabecular bone
(Figure 4, middle panel). Length
measurements were obtained from the cadaveric pelvis with an electromagnetic
digitizer (Immersion Corp, accuracy ±85 mm).
Measurements were based on identifiable anatomical features of the iliac
wing, ischium, obturator foramen, pubis, and acetabulum (Figure 4, left
panel). Excellent agreement was observed
between experimental measurements and the FE mesh dimensions, yielding a total
error of less than 3% (Figure 4, right panel).
Subject-specific Modeling of the Mechanics of the
Pelvis. Deformation of the pelvis can have a dramatic
influence on contact stresses at the hip (see, e.g., [1]). To assess
the ability of subject-specific FE models to predict cortical bone strains, a
combined experimental/computational study was pursued. The objectives of this study were to 1)
develop and validate a FE model of the pelvis using subject-specific
measurements of bone geometry as well as location-dependent cortical thickness
and trabecular bone elastic modulus, and 2) assess the sensitivity of the
subject-specific FE model by altering assumed and measured model inputs.
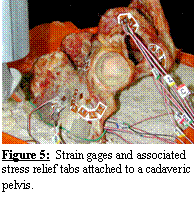Ten rosette strain
gauges (Vishay
Measurements Group, Raleigh, NC) were attached to a cadaveric hemi-pelvis
at locations around the acetabulum, pubis, ischium, and ilium (Figure 5) to
measure cortical bone strain during acetabular experimental loading [4]. A
registration block and wires were attached to the iliac crest. The block allowed for spatial registration of
experimental and FE coordinate systems, while the wires served as a guide to
reproduce the boundary conditions used in the experimental model [70]. The iliac crests were submerged in a mounting
pan of quick-setting cement to the depth defined by the iliac guide wires. Vertically orientated loads (0.25, 0.50,
0.75, and 1.0 BW) were applied to the acetabulum via a femoral prosthesis
attached to a linear actuator, while strains were recorded continuously.
The FE model was based on the mesh
shown in Figure 4. A 4-node, 24 degree
of freedom tetrahedral element was used to represent trabecular bone [5] (3 translational and 3 rotational degrees of freedom
at each node). Cortical bone was
represented with quadratic 3-node shell elements [6]. The elements
were based on the Hughes-Liu shell [7,8], which has three translational and rotational degrees
of freedom per node, with selective-reduced integration to suppress zero-energy
modes [9]. Acetabular
cartilage was modeled with the same type of shell elements. Initial material properties for cortical bone
and cartilage were taken from the literature, while relationships between CT
scanner intensity and density (as determined using a calcium equivalent bone
mineral phantom) were used to assign a density-dependent modulus to each
element. FE analyses were conducted
using the implicit capabilities of LS-DYNA
(Livermore Software Technology Corporation,
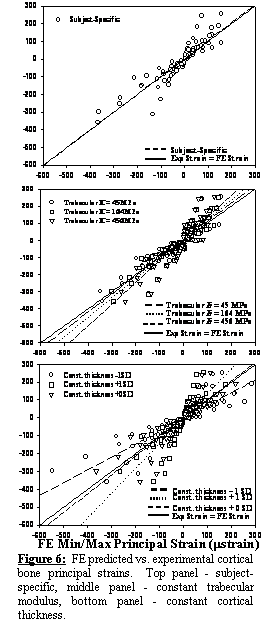The
subject-specific FE model predictions of principal strains showed excellent
correlation with experimental measurements, with a best-fit line that was
not significantly different than the line y = x (Exp. strain = FE
strain) (Figure 6, top). Models
representing changes to the trabecular bone elastic modulus did not alter
strains considerably (Figure 6, middle).
In contrast, changes in cortex thickness and cortical bone elastic
modulus had a substantial effect on cortical strains (Figure 6, bottom). Changes to all other material parameters did
not alter cortical strains significantly.
Using a sensitivity parameter it was determined that the pelvic FE mesh
was 10 times more sensitive to changes in cortical bone thickness than changes
to trabecular bone elastic modulus. This
finding illustrates the importance of including location dependent cortical
bone thickness to ensure accurate estimates of patient-specific biomechanics.
Experimental
Measurement and Finite Element Prediction of Cartilage Contact Stresses in the
Hip. Both
cartilage geometry and predictions of cartilage stresses play critical roles in
overall hip joint biomechanics. A
preliminary study was conducted to demonstrate our ability to accurately
predict cartilage contact stresses with the FE method. All soft tissue with the exception of
articular cartilage was removed from a 57 year-old male cadaveric pelvis and
femur. Kinematic blocks were attached to
both bones for purposes of referencing load and boundary conditions. The pelvis was loaded through the acetabulum
as described above. Super-low pressure
sensitive film (range 0.4 - 3.0 MPa, Sensor Products Inc.) was cut into a
rosette pattern [10] and placed on the femoral cartilage between layers of
thin polyethylene wrap. A 1 X BW load
was applied to the pelvis over 1 second through a linear actuator with attached
femur. The loading protocol was repeated
3 times with a new sheet of pressure sensitive film for each test. Anatomical points were digitized on the films
to provide reference locations. The film
was calibrated immediately following experimental testing.
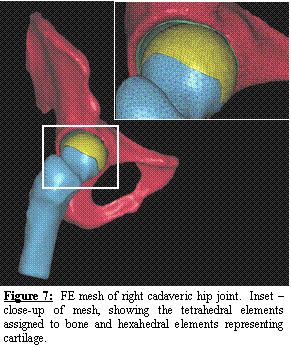A
volumetric CT scan (0.6 mm slice thickness) was acquired. The resulting images were segmented
semi-automatically using Amira. By replacing the manual segmentation
described above with the semi-automatic segmentation, the time required for
segmentation and mesh generation has been reduced from 2 weeks to less than 2
days! The femur and pelvis were meshed with
24 degree of freedom tetrahedral elements (Figure 7). Cortical bone was represented using quadratic
3-node shell elements [6-8] with position dependent thickness. Cartilage was represented with hexahedral
elements (Figure 7). Frictionless contact was enforced between the
cartilage while tied contact was enforced for the boundary between cartilage
and cortical bone. A position dependent
trabecular bone modulus was assigned.
The cartilage was represented as
elastic, isotropic, and homogenous [11,12] with material coefficients taken from the literature [13]. Although
cartilage is a biphasic material [14,15], the short-term response of a biphasic material to
loading is equivalent to the response of an incompressible elastic material [11,16]. Contact
stress measurements with pressure-sensitive film yield the total stress at the
articular surface (fluid pressure + solid matrix elastic stress) at the instant
of contact, which are equivalent to the contact stress from an incompressible
elastic analysis [17]. A sensitivity
study was conducted to explore the effects of bone deformation on cartilage
contact stresses.
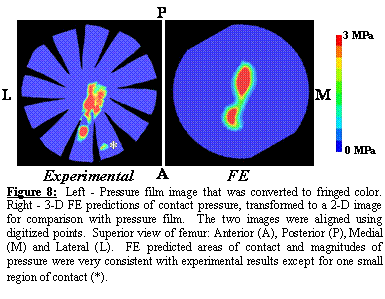The
three sheets of pressure film appeared nearly identical to one another after
each applied load. Contact pressures
ranged from 0 – 3 MPa (upper limit of film detection). FE model predicted contact pressures were in
excellent agreement with experimental results (range 0 – 5.5 MPa) (Figure
8). There was only one small area of
contact that was present in all of the experimental pressure film images, which
did not occur in the FE model predictions.
It is likely that this area of contact was due a small bony protrusion
that was not included in the FE model after smoothing. When the bone was modeled as rigid, cartilage
contact pressures reached a maximum of 7.9 MPa (43% higher than the original FE
model). Areas of cartilage contact for
the rigid bone model were noticeably different than the model that assumed
bones to be deformable.
Objective
2 – Patient-Specific FE Modeling of Acetabular Dysplasia (ongoing work)
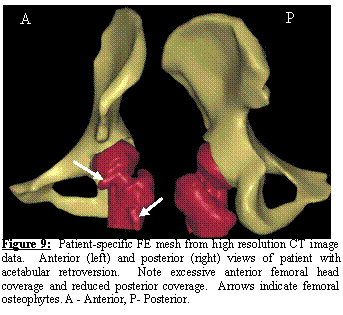Generation of Patient-specific Models of the Hip and Pelvis
from
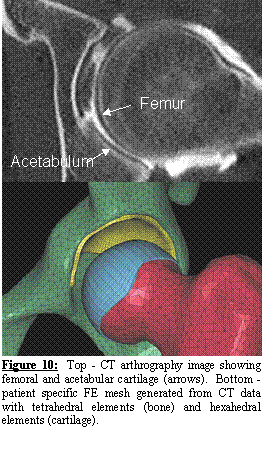A second normal subject was scanned with CT
arthrography. The subject’s hip joint
was injected with contrast agent under fluoroscopic control. Both the acetabular and femoral cartilage
were easily distinguishable in the resulting CT images (Figure 10, top). The cartilage layers were segmented and
meshed with hexahedral elements while the femur and pelvis were automatically
meshed with tetrahedral elements (Figure 10, bottom). We now have IRB approval to perform CT
arthrograms on both normal and dysplastic subjects, and have begun to recruit
subjects for patient-specific FE modeling of acetabular dysplasia.
References
[1] Bay, B. K.,
Hamel, A. J., Olson, S. A., and Sharkey, N. A., 1997, "Statically
Equivalent Load and Support Conditions Produce Different Hip Joint Contact
Pressures and Periacetabular Strains," J Biomech, 30, pp. 193-6.
[2] Prevrhal,
S., Engelke, K., and Kalender, W. A., 1999, "Accuracy Limits for the Determination
of Cortical Width and Density: The Influence of Object Size and Ct Imaging
Parameters," Phys Med Biol, 44, pp. 751-64.
[3] Prevrhal,
S., Fox, J. C., Shepherd, J. A., and Genant, H. K., 2003, "Accuracy of
Ct-Based Thickness Measurement of Thin Structures: Modeling of Limited Spatial
Resolution in All Three Dimensions," Med Phys, 30, pp. 1-8.
[4] Dalstra,
M., Huiskes, R., and van Erning, L., 1995, "Development and Validation of
a Three-Dimensional Finite Element Model of the Pelvic Bone," J Biomech
Eng, 117, pp. 272-8.
[5] Pawlak,
T. P. and Yunus, S. M., 1991, "Solid Elements with Rotational Degress of
Freedom: Part Ii Tetrahedron Elements," International Journal for
Numerical Methods in Engineering, 31, pp. 593-610.
[6] Ahmad,
S., 1970, "Analysis of Thick and Thin Shell Structures,"
International Journal for Numerical Methods in Engineering, 2, pp. 419-451.
[7] Hughes,
T. J. and Liu, W. K., 1981,"Nonliner Finite Element Analysis of Shells:
Part I. Two Dimensional Shells.," in Compuational
Methods in Applied Mechanics, vol. 27,
pp. 167-181.
[8] Hughes,
T. J. and Liu, W. K., 1981,"Nonlinear Finite Element Analysis of Shells:
Part Ii. Three Dimensional Shells.," in Computational Methods in Applied Mechanics, vol. 27, pp. 331-362.
[9] Hughes,
T. J., 1980,"Generalization of Selective Integration Procedures to
Anisotopic and Nonlinear Media," in Interational
Journal for Numerical Methods in Engineering, vol. 15, pp. 9.
[10] von
Eisenhart-Rothe, R., Eckstein, F., Muller-Gerbl, M., Landgraf, J., Rock, C.,
and Putz, R., 1997, "Direct Comparison of Contact Areas, Contact Stress
and Subchondral Mineralization in Human Hip Joint Specimens," Anat Embryol
(Berl), 195, pp. 279-88.
[11] Armstrong,
C. G., Lai, W. M., and Mow, V. C., 1984, "An Analysis of the Unconfined
Compression of Articular Cartilage," J Biomech Eng, 106, pp. 165-73.
[12] Eberhardt,
A. W., Keer, L. M., Lewis, J. L., and Vithoontien, V., 1990, "An
Analytical Model of Joint Contact," J Biomech Eng, 112, pp. 407-13.
[13] Shepherd,
D. E. and Seedhom, B. B., 1999, "The 'Instantaneous' Compressive Modulus
of Human Articular Cartilage in Joints of the Lower Limb," Rheumatology
(Oxford), 38, pp. 124-32.
[14] Mow,
V. C. and Lai, W. M., 1980, "Recent Developments in Synovial Joint Biomechanics,"
Soc Ind. Appl. Math. Rev, 22, pp. 275-317.
[15] Mow,
V. C., Kuei, S. C., Lai, W. M., and Armstrong, C. G., 1980, "Biphasic
Creep and Stress Relaxation of Articular Cartilage in Compression? Theory and
Experiments," J Biomech Eng, 102, pp. 73-84.
[16] Mak,
A. F., Lai, W. M., and Mow, V. C., 1987, "Biphasic Indentation of
Articular Cartilage--I. Theoretical Analysis," J Biomech, 20, pp. 703-14.
[17] Ateshian,
G. A., Lai, W. M., Zhu, W. B., and Mow, V. C., 1994, "An Asymptotic
Solution for the Contact of Two Biphasic Cartilage Layers," J Biomech, 27,
pp. 1347-60.
Acknowledgements
Financial support from the
ABSTRACTS
POSTER
ORIGINAL RESEARCH ARTICLE
OTHER LINKS
Finite Element Tools Home Page
- Helpful FE tools for working with LS-DYNA
OREF Home
Page - Orthopedic Research and Education Foundation
|
Created by |
|
|
For |
