This brings us to the notion of cache-rings. For any given voxel, v[i,j,k], in order to generate the portion of the surface that intersects that cell, we only need the scalar field data at the corners of the cell, and the shared-edge intersection information from the previously visited voxels: v[i,j,k-1], v[i,j-1,k], v[i,j-1,k-1], v[i-1, j, k], v[i- 1,j,k-1], and v[i-1, j-1,k]. These voxels and edges are shown in Figure 1.
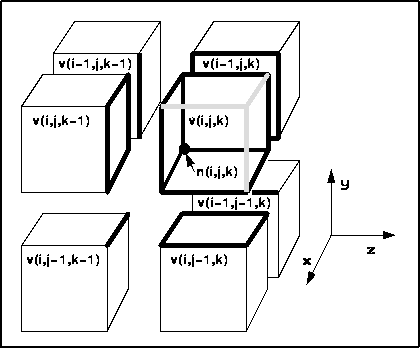
Figure 1: Previously visited, neighboring voxels. The thick, dark lines indicate edges shared with the current voxel, v[i,j,k]. The location of the node n[i,j,k] is indicated with a dark point. The lighter gray lines on the current voxel indicate edges which have not yet been encountered, and whose intersection nodes might, therefore, need to be computed. Thinner lines indicate all other voxel edges - none of these are of interest when extracting at the current voxel.
The edge information from each direction is stored in a data-structure called a ``cache-ring.'' Each ring is implemented as a ring-buffer, and stores edge intersection information for the neighboring cells of a particular direction. We note that each ring has a maximum length equal to the the number of cells traversed between that neighboring voxel and the current voxel. For example, voxel v[i,j-1,k] is (nz-1) voxels away from the current voxel v[i,j,k]; therefore, the ring in the y-direction, the y-ring, needs to have a maximum of nz entries (both sides of the current voxel need to be stored, which increases the total by one entry). We traverse the data in normal Marching Cubes fashion, and upon completing each voxel, we record the current information into all of the rings and advance the pointers. A graphical depiction of three of these rings is shown in Figure 2.
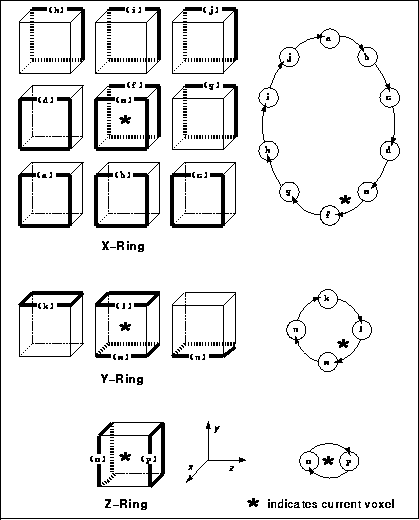
Figure 2: The X-, Y-, and Z-Rings and their contents during data traversal. The left side of each ring shows the currently active edges whose data is stored in the ring. As indicated by the axes, the cells are visited from left to right, from top to bottom, and from back to front. The right side of each diagram depicts the cache-ring storing the edge information, with arrows indicating the direction of traversal.
In practice, we actually utilize only a small portion of each ring at a time for storing precomputed indices - most of the voxels between the current voxel and the last voxel in the ring contain no intersection points, and are empty. Recognizing that ring data is always accessed deterministically (every entry which is stored is guaranteed to be accessed, and the accesses will occur in exactly the same order in which they are stored), we only need to store those edges which contain an intersection. With this revised implementation, we now store two indices into each ring - one for the voxel being examined and one for the neighbor information being stored (previously, these indices were identical, so a single value was sufficient). New data is always inserted at the last index, and the next intersection index is always read from the head.