


Active Shape Model
Wei Liu (u0614581)
weiliu@sci.utah.edu
Date: March 12, 2010
This report presents how I implement Active Shape Model - a method
using principal component analysis for feature extraction, and
dimension reduction.
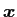 is used as vectors, and
is used as vectors, and 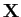 is used as matrics.
is used as matrics.
Get principal components: The ASM method assume an multivariate vector
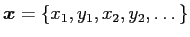 . If the original number of landmarks are
. If the original number of landmarks are 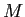 , the data vector will be
, the data vector will be 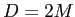 . To capture the principal components (i.e. the major modes, as stated in Cootes et al. (1998)), we use PCA and have eigen-decomposition on the covariance matrix
. To capture the principal components (i.e. the major modes, as stated in Cootes et al. (1998)), we use PCA and have eigen-decomposition on the covariance matrix 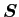 of
of 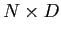 data matrix
data matrix 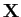 , which has each row as multivariate observation. The convariance matrix S is given by
, which has each row as multivariate observation. The convariance matrix S is given by
The eigenvalue decomposition of convariance 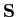 is
is
where 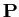 's columns are the eigenvectors of
's columns are the eigenvectors of 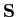 , and
, and 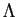 is diagonal matrix with diagonal the eigen value of
is diagonal matrix with diagonal the eigen value of 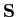 .
.
Projection to principal components: We can get the new coordinates (a.k.a the feature vectors) by projecting data vector 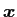 to this new basis vectors and get
to this new basis vectors and get
meaning the coordinates of data vector 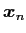 projected on the
projected on the 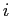 th principal component
th principal component 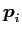 .
.
synthetic data from principle components: We can use a 'generative model', to generate synthetic data from mean vector
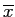 and principal components
and principal components
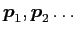
where
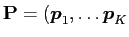 is the first
is the first 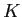 th components, and
th components, and
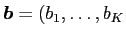 is the weights. We use
is the weights. We use
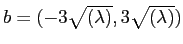 .
.
Random tranlations: I begin the test with random translations without noisey perturbation. I use a rectangular as a base shape, and use 12 landmarks on the contour. The coordinates of landmarks are added with random number of Gaussian distribution
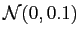 . To make sure the translations along all direction in a isotropic way, I add different, indepent random noise on
. To make sure the translations along all direction in a isotropic way, I add different, indepent random noise on 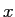 coordinates, and
coordinates, and 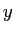 coordinates respectively. 100 sample shapes were generated.
coordinates respectively. 100 sample shapes were generated.
The results in Fig.1 shows that the principal components are able to catch the most significant variance in original data samples. I see most of the variances are in the first two eigen values, and this is consistent with the fact that translation have two degree of fredom (in two orthogonal directions). The reconstructed synthetic shape indicate the major modes along those two directions. The correlation map is linearly scaled to 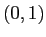 for visualization purpose. The checkerboard-like correlation map shows that all the
for visualization purpose. The checkerboard-like correlation map shows that all the 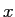 coordinates are strong correlated, and the correlation between
coordinates are strong correlated, and the correlation between 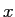 and
and 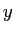 coordinates are low. This is consistent with our understanding, because during translation, all
coordinates are low. This is consistent with our understanding, because during translation, all 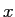 coordinates are offset by same number, but the change of
coordinates are offset by same number, but the change of 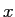 and
and 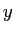 coordinates are independent.
coordinates are independent.
Figure 1:
Shapes translated. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 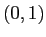 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 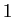 ,
, 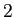 and
and 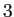 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
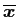 , red is
, red is
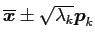 , and green is
, and green is
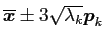 .
.
|
Random scaling: All the coordinates in 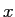 are multiplied by same scaling factor
are multiplied by same scaling factor 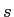 , which is a random number of Gaussian distribution
, which is a random number of Gaussian distribution
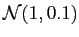 .
.
The results in Fig.2 shows one one eigenvalue are significantly greater than zero. This is because random scaling only have one degree of freedom, and one component is enough to capture the change. Not like translation, the correlation map is hard to say something.
Figure 2:
Shapes scaled. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 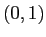 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 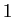 ,
, 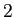 and
and 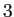 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
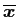 , red is
, red is
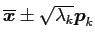 , and green is
, and green is
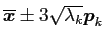 .
.
|
Random translation and scaling: we first translate the shape then scale them. Fig.3 shows that the first three components capture most of the variance. This is because tranlation and scaling together have three degree of freedom. This can also be showned in the second row of Fig.3, where the first two synthetic shape represent the variance of translation, and the third represents scaling. The correlation map looks like the combination of the one in previous two scenarios.
Figure 3:
Shapes translated and then scaled. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 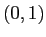 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 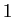 ,
, 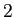 and
and 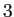 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
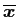 , red is
, red is
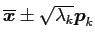 , and green is
, and green is
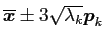 .
.
|
Random translationns, scalings with noise: See Fig.4, 5 and 6 for the counterparts of Fig.1, 2, and 3, but with additive noise. The noise is added to each elements of data vector 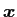 , which means the shape after adding noise is never a rectangular shape, because of the different noise added on each
, which means the shape after adding noise is never a rectangular shape, because of the different noise added on each 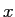 coordinate in a single shape.
coordinate in a single shape.
In Fig.4 I see the principal compoents are still able to capture the variance. The only difference is the orientation of the variance. This is probably because I add isotropic Gaussian noise, and the basis vector in the subspace is not unique, as long as they are orthogonal to each other. However I need a more rigid explination about this.
In fig.6 we see the first component capture both the variance caused by scaling and translation, while component 3 only capture the remaining variance of scaling. This tell me we should not trust PCA too much when explaining the meaning of variance represented by each principal component.
Overall, the noised data have eigen value more spreaded along all components, instead of just concentrating on the first two or three. This is because when the data are perturbed with noise, the modes are not siginificant towards pure scaling, or translating.
Figure 4:
Shapes translated then add noise. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to  . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 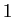 ,
, 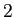 and
and 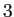 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
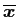 , red is
, red is
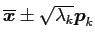 , and green is
, and green is
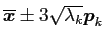 .
.
|
Figure 5:
Shapes scaled then add noise. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 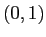 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 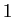 ,
, 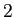 and
and 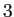 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
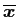 , red is
, red is
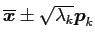 , and green is
, and green is
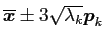 .
.
|
Figure 6:
Shapes translated and then scaled, and then add noise. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 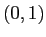 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 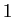 ,
, 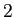 and
and 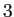 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
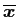 , red is
, red is
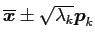 , and green is
, and green is
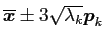 .
.
|
Rotation with noise: To generate rotated data, I first generate a random number 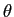 with
with
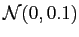 distribution, and apply 2D rotation matrix on
distribution, and apply 2D rotation matrix on 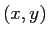 pairs of coordinates. The generated shapes and eigen-decomposition are in Fig.7. We see the synthetic shape represent the rotation, but with slightly skew.
pairs of coordinates. The generated shapes and eigen-decomposition are in Fig.7. We see the synthetic shape represent the rotation, but with slightly skew.
Figure 7:
Shapes rotated and then add noise. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 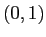 . Bottom from left to right: synthetic shape using the three principal components
. Bottom from left to right: synthetic shape using the three principal components 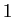 ,
, 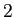 and
and 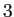 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
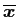 , red is
, red is
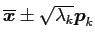 , and green is
, and green is
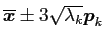 .
.
|
Copus callosum data: Run the algorithm on Copus callosum and get results in Fig. 8. I find in order to capture 90% of the variance in the data, we need at least 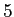 components.
components.
Figure 8:
Copus callosum data. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to 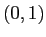 . Second row from left to right: synthetic shape using the three principal components
. Second row from left to right: synthetic shape using the three principal components 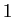 ,
, 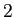 and
and 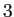 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
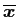 , red is
, red is
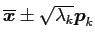 , and green is
, and green is
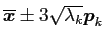 . Third row is component 4 and 5.
. Third row is component 4 and 5.
|
Handshapes data: For this data set I find four components is enough for a 90% variance.
Figure 9:
handshapes data. Top from left to right: the sample shape; eigenvalue; Correlation map scaled to  . 2nd row from left to right: synthetic shape using the three principal components
. 2nd row from left to right: synthetic shape using the three principal components  ,
, 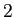 and
and 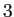 . In each sub-plot the blue is mean shape
. In each sub-plot the blue is mean shape
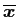 , red is
, red is
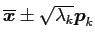 , and green is
, and green is
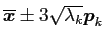 . bottom row is comp 4.
. bottom row is comp 4.
|
Very good method for feature extraction. When I generate the data with additive Gaussian noise, I remember about a probabilistic version of PCA Bishop et al. (2006), that reformulate PCA in a probabilistic framework. This seems promising.
-
C. M Bishop et al.
- Pattern recognition and machine learning.
Springer New York:, 2006.
-
T.F. Cootes, G.J. Edwards, and C.J. Taylor.
- Active appearance models.
In Computer Vision — ECCV’98, page 484. 1998.
URL http://www.springerlink.com/content/rkj17l4d3wen7tlm.



Wei Liu
2010-04-01
![]() is used as vectors, and
is used as vectors, and ![]() is used as matrics.
is used as matrics.
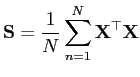
![]() to this new basis vectors and get
to this new basis vectors and get
![]() and principal components
and principal components
![]()
![]() for visualization purpose. The checkerboard-like correlation map shows that all the
for visualization purpose. The checkerboard-like correlation map shows that all the ![]() coordinates are strong correlated, and the correlation between
coordinates are strong correlated, and the correlation between ![]() and
and ![]() coordinates are low. This is consistent with our understanding, because during translation, all
coordinates are low. This is consistent with our understanding, because during translation, all ![]() coordinates are offset by same number, but the change of
coordinates are offset by same number, but the change of ![]() and
and ![]() coordinates are independent.
coordinates are independent.
![\includegraphics[width = 0.24\textwidth]{toyT.eps}](img37.png)
![\includegraphics[width = 0.24\textwidth]{toyT_ev.eps}](img38.png)
![\includegraphics[width = 0.24\textwidth]{toyT_corr.eps}](img39.png)
![\includegraphics[width = 0.24\textwidth]{toyT_comp1_rec.eps}](img40.png)
![\includegraphics[width = 0.24\textwidth]{toyT_comp2_rec.eps}](img41.png)
![\includegraphics[width = 0.24\textwidth]{toyT_comp3_rec.eps}](img42.png)
![]() are multiplied by same scaling factor
are multiplied by same scaling factor ![]() , which is a random number of Gaussian distribution
, which is a random number of Gaussian distribution
![]() .
.
![\includegraphics[width = 0.24\textwidth]{toyS.eps}](img45.png)
![\includegraphics[width = 0.24\textwidth]{toyS_ev.eps}](img46.png)
![\includegraphics[width = 0.24\textwidth]{toyS_corr.eps}](img47.png)
![\includegraphics[width = 0.24\textwidth]{toyS_comp1_rec.eps}](img48.png)
![\includegraphics[width = 0.24\textwidth]{toyS_comp2_rec.eps}](img49.png)
![\includegraphics[width = 0.24\textwidth]{toyS_comp3_rec.eps}](img50.png)
![\includegraphics[width = 0.24\textwidth]{toyTS.eps}](img51.png)
![\includegraphics[width = 0.24\textwidth]{toyTS_ev.eps}](img52.png)
![\includegraphics[width = 0.24\textwidth]{toyTS_corr.eps}](img53.png)
![\includegraphics[width = 0.24\textwidth]{toyTS_comp1_rec.eps}](img54.png)
![\includegraphics[width = 0.24\textwidth]{toyTS_comp2_rec.eps}](img55.png)
![\includegraphics[width = 0.24\textwidth]{toyTS_comp3_rec.eps}](img56.png)
![]() , which means the shape after adding noise is never a rectangular shape, because of the different noise added on each
, which means the shape after adding noise is never a rectangular shape, because of the different noise added on each ![]() coordinate in a single shape.
coordinate in a single shape.
![\includegraphics[width = 0.24\textwidth]{toyTN.eps}](img57.png)
![\includegraphics[width = 0.24\textwidth]{toyTN_ev.eps}](img58.png)
![\includegraphics[width = 0.24\textwidth]{toyTN_corr.eps}](img59.png)
![\includegraphics[width = 0.24\textwidth]{toyTN_comp1_rec.eps}](img60.png)
![\includegraphics[width = 0.24\textwidth]{toyTN_comp2_rec.eps}](img61.png)
![\includegraphics[width = 0.24\textwidth]{toyTN_comp3_rec.eps}](img62.png)
![\includegraphics[width = 0.24\textwidth]{toySN.eps}](img63.png)
![\includegraphics[width = 0.24\textwidth]{toySN_ev.eps}](img64.png)
![\includegraphics[width = 0.24\textwidth]{toySN_corr.eps}](img65.png)
![\includegraphics[width = 0.24\textwidth]{toySN_comp1_rec.eps}](img66.png)
![\includegraphics[width = 0.24\textwidth]{toySN_comp2_rec.eps}](img67.png)
![\includegraphics[width = 0.24\textwidth]{toySN_comp3_rec.eps}](img68.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN.eps}](img69.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN_ev.eps}](img70.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN_corr.eps}](img71.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN_comp1_rec.eps}](img72.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN_comp2_rec.eps}](img73.png)
![\includegraphics[width = 0.24\textwidth]{toyTSN_comp3_rec.eps}](img74.png)
![]() with
with
![]() distribution, and apply 2D rotation matrix on
distribution, and apply 2D rotation matrix on ![]() pairs of coordinates. The generated shapes and eigen-decomposition are in Fig.7. We see the synthetic shape represent the rotation, but with slightly skew.
pairs of coordinates. The generated shapes and eigen-decomposition are in Fig.7. We see the synthetic shape represent the rotation, but with slightly skew.
![\includegraphics[width = 0.24\textwidth]{toyRN.eps}](img78.png)
![\includegraphics[width = 0.24\textwidth]{toyRN_ev.eps}](img79.png)
![\includegraphics[width = 0.24\textwidth]{toyRN_corr.eps}](img80.png)
![\includegraphics[width = 0.24\textwidth]{toyRN_comp1_rec.eps}](img81.png)
![\includegraphics[width = 0.24\textwidth]{toyRN_comp2_rec.eps}](img82.png)
![\includegraphics[width = 0.24\textwidth]{toyRN_comp3_rec.eps}](img83.png)
![\includegraphics[width = 0.24\textwidth]{copus.eps}](img85.png)
![\includegraphics[width = 0.24\textwidth]{copus_ev.eps}](img86.png)
![\includegraphics[width = 0.24\textwidth]{copus_corr.eps}](img87.png)
![\includegraphics[width = 0.24\textwidth]{copus_comp1_rec.eps}](img88.png)
![\includegraphics[width = 0.24\textwidth]{copus_comp2_rec.eps}](img89.png)
![\includegraphics[width = 0.24\textwidth]{copus_comp3_rec.eps}](img90.png)
![\includegraphics[width = 0.24\textwidth]{copus_comp4_rec.eps}](img91.png)
![\includegraphics[width = 0.24\textwidth]{copus_comp5_rec.eps}](img92.png)
![\includegraphics[width = 0.24\textwidth]{hands.eps}](img93.png)
![\includegraphics[width = 0.24\textwidth]{hands_ev.eps}](img94.png)
![\includegraphics[width = 0.24\textwidth]{hands_corr.eps}](img95.png)
![\includegraphics[width = 0.24\textwidth]{hands_comp1_rec.eps}](img96.png)
![\includegraphics[width = 0.24\textwidth]{hands_comp2_rec.eps}](img97.png)
![\includegraphics[width = 0.24\textwidth]{hands_comp3_rec.eps}](img98.png)
![\includegraphics[width = 0.24\textwidth]{hands_comp4_rec.eps}](img99.png)