Contour Description by Fourier Harmonics

Wei Liu (u0614581)
weiliu@sci.utah.edu

Date: March 12, 2010

Contents

• introduction
• Methods
• Experiment Results and Analysis
• Discussion
• Bibliography

introduction

In this work I use real notation for Fourier harmonics analysis. Using method of Kuhl and Giardina, I compute Fourier series coefficients and reconstructed contours. Also computed the coefficients invariant of starting point, rotation, scaling. reconstructed contours with different number of harmonic components are shown. A short discussion is followed on the issues I found during implementation.

Methods

Computing Fourier coefficients: First, $\Delta t_i$ , $\Delta x_i$ and $\Delta y_i$ are computed by the method in the paper. Then $t_p$ , $x_p$ and $y_p$ are computed from the previously computed $\Delta$ value. It is noted from original formula of computing $\Delta t_i$ in the paper, it looks the author assume the constant spedd is $1$ . Therefore, the time needed to traverse a particular link $a_i$ is equal to the length of the link.

After this step we have Fourier coefficients $a_n$ , $b_n$ for coordinates $x$ , and coefficients $a_n$ , $b_n$ for coordinates $y$ . DC components $A_0$ and $C_0$ can also be obtained in similar way.

reconstruction: Can be done by choosing different number of Fourier harmonics components and by inverse Fourier transform in the paper.

elliptic loci: Careful observation of $X_n$ and $Y_n$ (the $n$ th component of reconstructed contour indicate this is a elliptical shape. This can be shown by canceling the sine and cosine terms and get something like

$$\frac{p X_n^2 + q Y_n^2 + r X_n Y_n}{s} = 1$$

where $p, q, r, s$ are coefficients of the elliptical shape.

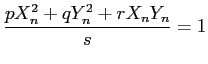Phase shift (starting point): The change of starting point does not change the reconstructed contour. It only change the phase of the sine and cosine. If we use $\lambda$ for the forward displacement between original starting point and new staring point, the relationship between $\lambda$ , and the change of phase $\theta_1$ of first component is $\theta_1 = \lambda * 2\pi/T$ , where $T$ is the period of the first harmonics.

The phase shift $\theta_1$ can be computed by the method of the paper, i.e. look at the derivative of the magnitude of first harmonics with respect to $\theta_1$ . once we get $\theta_1$ , we can use the relationship between original coefficients and $\lambda$ shifted coefficients, and get the new coefficients $a^*, b^*, c^*, d^*$ , which is the coefficients when starting point is located at semi-major axis.

Scaling invariant: is done by dividing all coefficients by the magnitude of semi-major axis.

Experiment Results and Analysis

Reconstruction: We first verify the first harmonics of a few contours, to see if it is elliptical. The results are at fig. 1. I did not connect the starting point and ending point on the reconstructed image on purpose, in order to show the location of the starting point. We can see the first harmonic correctly detect the basic shape of the image. If more harmonics are used, the reconstructed image will be better approximation of the original contour, as can be see from fig. 2.

Figure 1: Reconstructed contours from only the first harmonics. Red color is reconstructed contour. Blue color is the original

[vase] [house] [duck] [cat]

Figure 2: Reconstructed contours from five harmonics.

[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]

Changing starting point: We then test the reconstructed contour using $a^*, b^*, c^*, d^*$ , which is the coefficients for the starting point at semi-major axis. The results at fig. 3. Because I did not connect the starting point and ending point, it can be clear seen that the starting points are located at the semi-major axis.

Figure 3: Reconstructed contours from coefficients of starting point at semi-major axis. number of harmonics is 1, 5 and 10 from top to bottom.

[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]

rotated contour: After having rotation invariant coefficients, we use these coefficients to reconstruct contours. The reconstructed ones are all in a new coordinates system such that the positive $x$ is in the same direction with the semi-major axis of the ellipse. The results at fig. 4. Because there is ambiguity of the two possible orientation of the semi-major axis, I also plot another orientation with phase different $pi$ with fig. 4. The results at fig. 5.

Figure 4: Reconstructed contours from coefficients of rotation invariant . number of harmonics is 1, 5 and 10 from top to bottom.

[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]

Figure 5: Reconstructed contours from coefficients of rotation invariant . number of harmonics is 1, 5 and 10 from top to bottom.

[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]

Scale invariant: After dividing all the coefficients by the magnitude of semi-major axis, we get scale invariant coefficients. Fig. 6 has reconstructed contours from these rotation and scale invariant features.

Figure 6: Reconstructed contours from coefficients of rotation and scale invariant . number of harmonics is 1, 5 and 10 from top to bottom. For the two possibilities of rotation, only one of them are transformed to scale invariant.

[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]
[vase] [house] [duck] [cat]

Sum of difference: To see the difference of two contours, we can compare their Fourier coefficients. We use sum of squared difference between to set of coefficients. For the coefficients of $a, b, c, d$ , I just add them together. Because for each contours, there are two possible set of Fourier coefficients, for the two possible orientations. So the difference between two contours have four possible values. The minimal value among the four is a good choice to indicate the true difference between the two contours.

Table 1 and table 2 have the comparisons. If I look for a object most similar to 'house', one component and 20 component have different results: For one component, 'duck' is most similar to 'house'. For 20 components, 'vase' is the most similar.

Table 1: sum of difference among coefficients of different contours. Only one Fourider components are used.

	vase	house	cat	duck
vase
house	0.0578
cat	0.0033	0.0887
duck	0.0271	0.0058	0.0493

Table 2: sum of difference among coefficients of different contours. 20 Fourider components are used.

	vase	house	cat	duck
vase
house	0.1939
cat	0.1468	0.2874
duck	0.2650	0.2474	0.3252

Discussion

One issue I had is during reconstruction, I chose the time point $t$ same as the $t_p$ in computing Fourier coefficients. The results is the number of points in reconstructed contour is same as number of points in the original chain code, which lead to a over-discrete contour. Actually I found later that the $t$ in reconstructed formula is not related with $t_p$ . I can choose whatever interval that I want.

My conclusion is this is great tool for shape analysis, even from view of nowadays. Further, I think if we look at the image as 2-D signal, we can use many concepts and algorithms in signal processing, as DSP has long history and rich method. Fourier harmonics is only one of them.

No References!