Project 4: Feature detection

Carlos Eduardo Scheidegger
cscheid@cs.utah.edu
UID: 00454219

Abstract:

In this project, I implemented feature detection with the Hough transform. I investigated several forms of filtering and scale-space techniques, such as median filtering, gaussian filtering and anisotropic diffusion. Finally, I used clustering techniques to find the lines on a thresholded accumulator space.

Overview

For this final project, I implemented line detection. My implementation is pretty straight-forward. After prefiltering with an appropriate technique, I use the Canny and Marr-Hildreth edge detection to get binary images for the Hough transform. The hard part was to detect the features in the accumulator space. The approach I used was to create a binary version of the Hough transform with the high hits and then cluster that with a hierarchical clustering algorithm. The final clusters are then searched for high accumulation, and these points are transformed back into lines on the image space. In the next sections, I'll describe each of the steps in detail.

I implemented this technique as a sequence of small VISPack programs, so that I could experiment with the individual steps. The source code is provided in the code directory with the submission.

Edge detection

The two edge detection algorithm I used are based on zero-crossings of derivatives. Because of that, they are notoriously sensitive to noise. The usual solution is to prefilter the images or the kernel, whenever the edge-detection kernel is linear.

Marr-Hildreth detection

The first algorithm I'll discuss is the Marr-Hildreth edge detection. The idea is to compute the laplacian of an image, and then mark the zero-crossings of the laplacian as edges. One of the advantages of the Marr-Hildreth is the simplicity, and the fact that all edges detected are closed loops. The biggest problem is that it is extremely sensitive to noise. The usual solution is to convolve the kernel with a Gaussian. Some problems are alleviated, but the edges are then blurred and become more curved, hindering the line detection step further.

Figure 1: Running example.

Figure 2: Marr-Hildreth without filtering or thresholding. Notice the JPEG-compression artifacts

Figure 3: Marr-Hildreth with Gaussian filtering, $\sigma = 2$ and no thresholding.

Figure 4: Marr-Hildreth with Gaussian filtering, $\sigma = 2$ and thresholding $\vert\vert f\vert\vert > 3$.

With appropriate filtering and thresholding, the marr-hildreth does give surprisingly good results. The filtering is essential to get the edges at the correct scale. Unfortunately, it is easy to get parameters wrong:

Figure 5: Marr-Hildreth with badly tuned parameters.

Canny detection

I then experimented with another filter, the Canny edge filter. The idea of the canny edge filter is to detect maxima of gradient derivatives on the direction of the gradient. Canny also introduced the idea of hysteresis thresholding: using two thresholds and connected components to filter out noise. Since I'm using VISPack's implementation of the Canny edge detection, and it only takes a single threshold value, I imagine that the hysteresis threshold is not implemented.

For the Canny edge detection, I tried using two different forms of filtering: anisotropic diffusion and median filtering. The anisotropic diffusion seemed to work reasonably well, but the edges tended to be ``scruffier'': they are not as neat as the usual detection. I think that may be a bug in my use of VISPack's anisotropic filtering -- I don't think I could get the parameters to work nicely. Here, I'm using between 0.1 and 0.3 and 15 iterations of diffusion. What I found with AD is that I can use much higher thresholds and the results are still adequate.

Figure 6: Running Example

Figure 7: Canny edges without thresholding or filtering. Again the signal-to-noise ratio is small.

Figure 8: Canny edges with thresholding.

Figure 9: Anisotropic Diffusion of the previous figure

Figure 10: Canny edges without thresholding, after 15 iterations of anisotropic diffusion (k=0.1). Results are worse than without filtering.

Figure 11: Canny edges with threshold 3, after 15 iterations of anisotropic diffusion (k=0.1). Results are now adequate

Figure 12: Canny edges with threshold 10, after 15 iterations of anisotropic diffusion (k=0.1). This is to show AD allows higher thresholds.

Figure 13: Median-filtered image with window size 5.

Figure 14: Canny edges without thresholding, with median filtered-image above.

Figure 15: Canny edges with threshold and median-filtering.

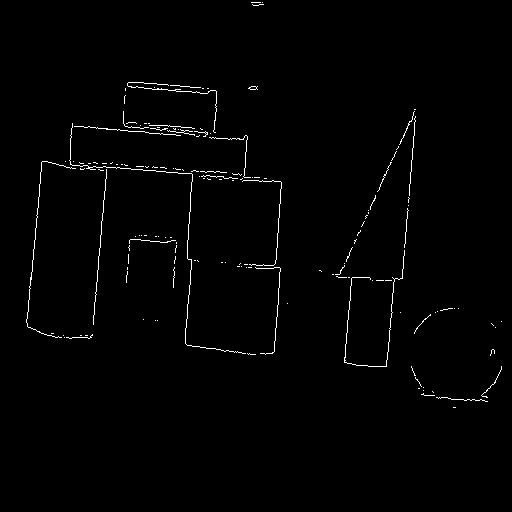It seems that median filtering works best for the tests I did. I'm sure that there's something wrong with my anisotropic diffusion, but I couldn't fix it. All in all, Canny edges seemed more robust, especially when there are many edges on the image, because Marr-Hildreth edge detection needs to work on a large scale to get rid of noise issues, and this also suppresses many legimitate edges.

The Hough transform

After detecting edges on the images, the main algorithm of the project is invoked. The Hough transform takes a binary image, and transforms every lit point in this image to a dual space, usually called the accumulator space. In this dual space, every point becomes a line (or a curve). The most important feature of the dual space is that points that are collinear in the primal space intersect at the same point in the dual space. Any dual point-line transformation works, but the normal equation duality is usually employed because of issues like unbounded values on the parameter space. In this dual transformation, one dimension (in our case, $y$)is the signed distance $\rho$ from the line to the origin. I normalize the image range to $[0,1]^2$, so $-\sqrt{2} \leq \rho \leq \sqrt{2}$. The other parameter is the normal of this line, which I call $\theta$. All lines can be represented uniquely using a range of only $\pi$ radians. I normalize the Hough space to $[0,1]^2$ by linear scaling.

Figure 16: The hough Transform of the previous figure. Darker points indicate higher accumulation.

To detect lines, I note that since the image and accumulator spaces are dual, a single point on the accumulator space indicates a line on image space. So I need only pick adequate points on the accumulator space and transform them back. It turns out that this is the hard part.

The accumulation space

For images with few edges or little noise, the accumulator space is reasonably well-behaved - the maxima can be picked out somewhat simply looking at local maxima and thresholding. I tried this first approach and it did work on simple images, but it didn't on more complex ones.

Figure 17: A synthetic square, its edges, and their Hough Transform

Figure 18: A synthetic polygon, its edges, and their Hough Transform

My second try was to successively pick global maxima and suppress the neighborhood (up to a certain percentage of the value on the accumulator space). This gave better results, but it was hard to tune the amount of suppression, since it changed a lot from image to image. My final implementation thresholds the accumulator space in a different way. I noticed that the points with high accumulation have markedly high gradients. They are not exactly edges, but edge detection algorithms should pick those up pretty easily. Then, the thresholding parameter could be used to filter out false positives. It turned out that rarely edge detection algorithms detect two closely parallel lines (unless they're there to begin with). This means that in the $y$ direction of the accumulation space, the gradient is usually close to the number of points accumulated in the line. Because of that, I threshold the Canny edge detection based on the expectation of the size of the minimum line. I used between 20 and 30 in the examples here.

After the edge detection in the Hough space, we end up with another binary image. Each of these points indicate a candidate for transforming back to lines in the image space. We should expect these points to be clustered together, and that is indeed the case:

Figure 19: The binary output of Canny edge detection on the accumulation space.

What is left to do is to cluster these points in coherent bundles, and use a single line for each of them. I implemented this by simple hierarchical clustering. Starting with each point representing a cluster, the algorithm try to find good matches in terms of distance in the parameter space. Instead of storing the entire complete graph (which could be $O(n^4)$ memory), I use a RANSAC-like algorithm where pairs of clusters are picked and tested. The best pair is then clustered if their similarity if above a certain threshold. If the pairs fail the similarity test, the algorithm terminates.

To implement this, we need a notion of distance in the accumulation space. I used an $\theta$ value ranging in $[0, \pi/2)$. This has the advantage of representing every line uniquely, but has a very interesting consequence. Since the other parameter in the accumulation space, $\rho$, gives the signed distance to the origin, two almost equal lines with opposite facing normals will be far apart from each other in a naïve distance measurement (the $\rho$ sign will be flipped). It turns out that the topology of this parameter space is exactly the one of the Möbius strip: after one walk across the $\theta$ parameter range, we end up with a negative $\rho$. To illustrate this, see this accumulation for the synthetic square.

Figure 20: The accumulation space, as defined, is non-orientable. Notice that a simple wrap-around topology will falsely make it look like there are six different clusters. The right border should be flipped once, and then ``glued'' to the left margin.

The distance measure on the parameter space, then, actually sums the two $\rho$ values if $\theta > \pi/2$. With such a definition, the clustering algorithm successfully finds only 4 clusters. Each cluster is then serached for the highest accumulation. Notice that we have to search neighboring pixels, because the clusters are actually made of edges. The transformation back to image space is straightforward.

Results

Synthetic Data

For synthetic data, the Hough transform worked extremely well. Not only few edge outputs from Canny edges make the Hough transform faster, but the absence of noise points cause the accumulation space to be clean, and then the clustering algorithm finds good results. The original image was darkened by 50%, and the detected lines are depicted in white.

Figure 21: Pipeline for the Hough transform on a synthetic square.

Figure 22: Pipeline for the Hough transform on a synthetic polygon.

Real Photographs

For real photographs, I usually found that median filtering followed by Canny detection with a small threshold or anisotropic diffusion followed by Canny detection with a large threshold gave best results. There was only one instance in which the Marr-Hildreth performed best, and that was with the Baboon image, where the Marr-Hildreth detection succesfully found the two main lines of the baboon's nose. Still, it required significant parameter tuning.

Figure 23: Tshape line detection with anisotropic diffusion and Canny edge detection.

Figure 24: Pentagon line detection with median filtering and Canny edge detection.

Figure 25: Arch line detection with 2 passes of anisotropic filtering and Canny edge detection.

Figure 26: Buildings line detection with 2 passes of anisotropic filtering and Canny edge detection.

Figure 27: Romebldg line detection with 10 iterations of 5-wide median filters and Canny edge detection.

Figure 28: Baboon line detection with anisotropic diffusion and Marr-Hildreth edge detection.

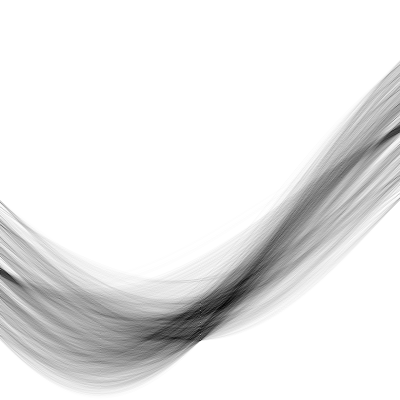
Most of the results are reasonable. There were some inexistent lines, like for example the diagonal lines on the buildings example, and the horizontal line in the bottom of the baboon. Still, I believe that my implementation got good results on a variety of images.

More work

My code should be easy to extend to general Hough transforms. I intended to do this, but ran out of time. Also, intelligent clipping of the lines should be easy in image space using SUSAN corner detection or something similar. Unfortunately, I'm already late again.

I also think my edge detection on the Hough transform is not that good. I can definitely pick out the maxima by eye, so I believe there has to be a way of doing it automatically. I'm pretty happy with the clustering algorithm, but if it gets wrong input data, it will output bad data (such as can be seen in the buildings example).

Conclusion

Hough transforms are seriously cool, especially because they're very efficient. If you have a fast sinusoid rasterizer (not my case :), the hough transform can be done in real-time. This makes it very useful for time-critical applications. The general Hough transforms seem very similar to matched filters, without having to go to the frequency domain, which may make sense in terms of performance.

Overall, I had a lot of fun coding these projects up throughout the semester, and it did give me a much deeper understanding of the subject than I would have had otherwise. It was a lot of work, but it was definitely worth it.

About this document ...

Project 4: Feature detection

This document was generated using the LaTeX2HTML translator Version 2002 (1.62)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -nonavigation index

The translation was initiated by Carlos Scheidegger on 2005-05-06