An interesting, but very challenging kind of imaging is to visualize the interior of a non-transparent object (such as a human body) using physical fields measured outside the body. This imaging is achieved through a mathematical engine known as "inverse problems solving" or "statistical optimization", one of the key research directions at the SCI Institute.
Another research direction being pursued at the SCI Institute is solving "ill-posed" imaging problems by constraining the solution with focusing criterion. This allows us to reconstruct sharp solutions out of smooth data. The process is made possible by selecting special stabilizing functions that permit sharp solutions. Applications of this technique range from bioelectric source localization utilizing magneto and electro -encephalography data for medical imaging, to geophysical inversions with gravity and magnetic fields.
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 |
Figure 1 shows an epileptic patient in a magneto encephalography (MEG) measuring array. Each quadratic plate is a sensor that measures properties of magnetic fields. The fields produced by the brain are very weak, so to measure them, the sensors are wrapped in a cryogenic coating which cools them down to superconducting temperature. There are two major applications of MEG. In functional studies, a subject is given a particular task. The brain activity is then measured to ascertain which regions of the brain are responsible for that particular task. The second are epileptic studies, such as the case shown here, where epileptogenic regions of the brain show spontaneous activity.
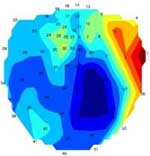
In figure 2, the MEG data for the patient from the previous figure at one instance in time is shown. The data is displayed as surface projections. Magnetic fields are recorded in a continuous time, but only a few relevant moments are analyzed by doctors.
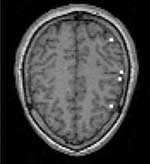
The dots in figure 3 show dipoles obtained from the data gained by the procedure. They were overlaid on an MRI image of the brain. The magnetic activity can be viewed as a response of the electric dipoles within the head. Once the locations of such dipoles are found, the inverse problem has been solved.
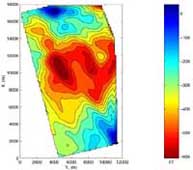
As previously stated, inverse problem solving can be applied to geophysical data as well. In the first figure below, magnetic data is gathered by means of an aircraft traveling approximately 200 meters above the ground. This allows a researcher to cover large areas in a short amount of time. Anomalies (maximums and minimums in the magnetic field) that are visible on this picture are produced by underground geological structures.
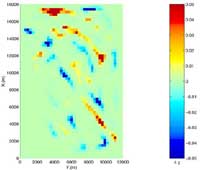
The Results are a focused inversion (magnetic susceptibility distribution). Figure 4 shows a single slice of the 3-dimensional inversion volume. In figure 5, this slice is taken at a depth of 500m. The darker structures visible here correspond to geological faults.
 |
 |
| Figure 4 | Figure 5 |
History
The development of the mathematical foundations that enable modern imaging began centuries ago with the fundamental notion of probability. This started with the works of Girolamo Cardano, a 16th century philosopher.Cardano observed a game of dice, and postulated that if a player throws the dice more times than his partner, he is cheating, and if less, he is a fool. In the 18th century, Thomas Bayes developed probability into a theory.
In 19th century, Carl Gauss invented "least-squares", a notion which is widely used in modern imaging and signal processing theory.
In 1902 Jacques Hadamard classified all mathematical problems into either "well-posed" or "ill-posed." He defined a "well-posed" problem as one with an existing, unique and well-conditioned solution. Such problems were considered to be solvable. If a problem is not proven to have an existing and unique solution, it is considered "ill-posed," or unsolvable.
In the 1930s, Andrei Kolmogorov formulated probability axiom as different outcomes of a repeatable experiment under the same conditions.
In the 1940s, mathematician Andrei Tikhonov, working on a theory of geophysical exploration, published a paper starting the development of "regularization theory," which considers ill-posed problems to be solvable and proposes methods for their solution.
